Class 12 Maths Chapter 13 MCQs with Answers Probability Free Download All chapter MCQs for class 12 Maths Exam Base Question.
Class 12 Maths Chapter 13 MCQs
1. Let A and B be two given events such that P(A) = 0.6, P(B) = 0.2 and P(A/B) = 0.5. Then P(A’/B’) is

Answer: c
2. Let A and B be two given independent events such that P(A) =p and P(B) = q and P(exactly one of A, B) = 23, then value of 3p + 3q – 6pq is
(a) 2
(b) -2
(c) 4
(d) -4
Answer: a
3. If P(A ∩ B) = 70% and P(B) = 85%, then P(A/B) is equal to {Class 12 Maths Chapter 13 MCQs }

Answer: a
4. Two dice are thrown once. If it is known that the sum of the numbers on the dice was less than 6 the probability of getting a sum 3 is

Answer: c
5. Three balls are drawn from a bag containing 2 red and 5 black balls, if the random variable X represents the number of red balls drawn, then X can take values
(a) 0, 1, 2
(b) 0, 1, 2, 3
(c) 0
(d) 1, 2
Answer : A
6. The probability distribution of the discrete variable X is given as:
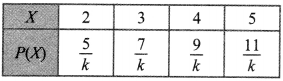
The value of k is
(a) 8
(b) 16
(c) 32
(d) 48
Answer: (C)
7. Let A and B be two given mutually exclusive events. Then P(A/B) is _________ .
Answer: 0
8. If A and B are two independent events such that P(A) = 17 and P(B) = 16 then P(A’ ∩ B’) is _________ .
Answer: 5/7
9. Three persons A, B and C, fire a target in turn. Their probabilities of hitting the target are 0.2,0.3 and 0.5 respectively, the probability that target hit is _________ .
Answer: 0.72
10. If A and B are independent events, then P(A and B) = P(A) + P(B). State true or false. Class 12 Maths Chapter 13 MCQs
Answer: False
11. A speaks truth in 70% cases and B speaks truth in 85% cases. The probability that they speak the same fact is ______ .
Answer: 64%
12. Given P(A) = 0.4, P(B) = 0.7 and P(B/A) = 0.6. Find P(A ∪ B).
Answer: 0.86
13. Given P(A) = 12 p(B) = 13 and P(A ∩ B) = 16. Are the events A and B independent?
Answer:
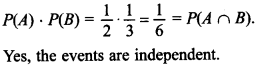
14. Prove that if E and F are independent events, then the events E and F are also independent. [Delhi 2017]
Answer:
As E and F are independent events
∴ P(E ∩ F) = P(E)P(F) …(i)
Consider,
P(E)P(F) = P(E)[1 – P(F)]
= P(E) – P(E)P(F)
= P(E) – P(E ∩ F)
P(E)P(F’) = P(E ∩ F’)
⇒ E and F’ are independent events.
15. A die, whose faces are marked 1, 2, 3 in red and 4,5,6 in green, is tossed. Let A be the event “number obtained is even” and B be the event “number obtained is red”. Find if A and B are independent events. [AI 2017]
Answer:
A : number is even, i.e. 2, 4, 6; P(A) = 36
= 12
B : number is red, i.e. 1, 2, 3; P(B) = 36
= 12
A ∩ B : number is even and red, i.e. 2;
P(A ∩ B) = 16
P(A) × P(B) = 12×12=14
As P(A ∩ B) ≠ P(A) . P(B)
Hence, not independent.
Class 12 Maths Chapter 13 MCQs
16. A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4. [CBSE 2018]
Answer:
A : sum 8, i.e. (2, 6), (3, 5), (4, 4), (5, 3), (6, 2)
B : red die number less than 4.
B : (1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (6, 2), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3).
A ∩ B : (6, 2), (5, 3)
∴ Conditional probability of obtaining sum 8, given that red die resulted in number less than 4.
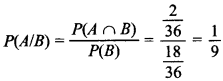
17. 12 cards numbered 1 to 12 are placed in a box, mixed up thoroughly and then a card is drawn at random from the box. If it is known that the number on the drawn card is more than 3, find the probability that it is an even number.
Answer:
Total cards are 12
A : number drawn is more than 3, i.e. 4, 5, 6, …, 12.
B : getting an even number, i.e. 2, 4, 6, 8, 10, 12.
A ∩ B : 4, 6, 8, 10, 12
18. One card is drawn from a well shuffled pack of 52 cards. If E is the event “the card drawn is a king or a queen” and F is the event “the card drawn is an ace or a queen,” then find the probability of the conditional event E/F. [HOTS]
Answer:

19. Two cards are drawn from a well shuffled pack of 52 cards one after the other without replacement. Find the probability that one of them is a queen and the other is a king of opposite colour.
Answer:
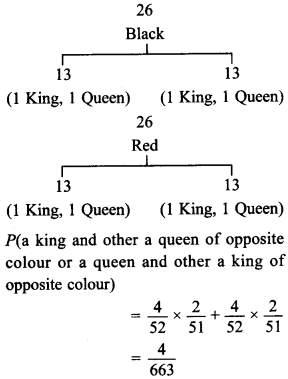
20. A coin is tossed thrice and all eight outcomes are assumed equally likely. Let the event E be “the first throw results in head” and event F be “the last throw results in tail”. Find whether events E and F are independent.
Answer:
Sample space
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
E: first throw results in head = {HHH,HHT,HTH,HTT}
F: Last throw result in tail = {HHT, HTT, THT, TTT}

21. Two dice are thrown. Find the probability that the numbers appeared have a sum 8 if it is known that the second die always exhibits 4. [HOTS]
Answer:
A: Sum of the numbers is 8, i.e. {(2,6), (3,5), (4,4), (5,3), (6,2)}
B: the second die always exhibits 4, i.e. {(1,4), (2,4), (3,4), (4,4), (5,4), (6,4)} A ∩ B= {(4, 4)}
Required probability,
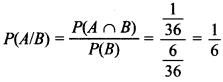
22. If P(A)=0.8,P(B)=0.5 andP(B/A)=0.4, find (i) P(A ∩ B) (ii) P(A/B) (iii) P(A ∪ B). [NCERT]
Answer:
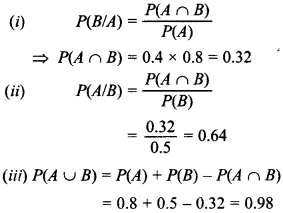
23. The value of k, for which the following distribution is a probability distribution

Answer:

24. Find mean (µ) and variance (a2) for the following probability distribution:
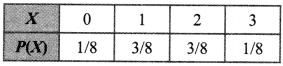
Answer:
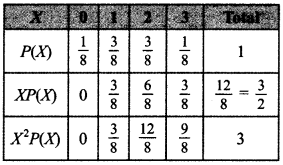
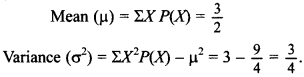
25. A random variable X has a probability distribution P(X) of the following form where k is some number:Determine (i) k (ii) P(X ≤ 2) (iii) P(X ≤ 2) (iv) P(X ≥ 2). [NCERT; Delhi 2019]
Answer:
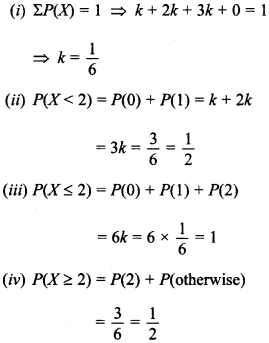
Class 12 Maths Chapter 13 MCQs
1. Let A and B be two given events such that P(A) = 0.6, P(B) = 0.2 and P(A/B) = 0.5. Then P(A’/B’) is

Answer: c
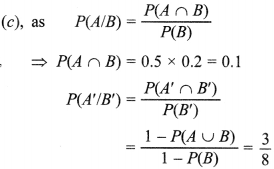
2. Let A and B be two given independent events such that P(A) =p and P(B) = q and P(exactly one of A, B) = 23, then value of 3p + 3q – 6pq is
(a) 2
(b) -2
(c) 4
(d) -4
Answer: a
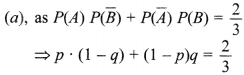
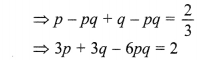
3. If P(A ∩ B) = 70% and P(B) = 85%, then P(A/B) is equal to

Answer: a
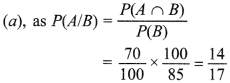
4. Two dice are thrown once. If it is known that the sum of the numbers on the dice was less than 6 the probability of getting a sum 3 is

Answer: c
as favourable cases for sum less than 6 are 10 and favourable for a total of 3 is 2.
5. Three balls are drawn from a bag containing 2 red and 5 black balls, if the random variable X represents the number of red balls drawn, then X can take values
(a) 0, 1, 2
(b) 0, 1, 2, 3
(c) 0
(d) 1, 2
Answer : A
6. The probability distribution of the discrete variable X is given as:

The value of k is
(a) 8
(b) 16
(c) 32
(d) 48
Answer:
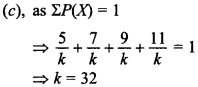
7. Let A and B be two given mutually exclusive events. Then P(A/B) is _________ .
Answer:
0, as P(A ∩ B) = 0 and P(A/B) = P(A∩B)P(B)
8. If A and B are two independent events such that P(A) = 17 and P(B) = 16 then P(A’ ∩ B’) is _________ . Class 12 Maths Chapter 13 MCQs
Answer:
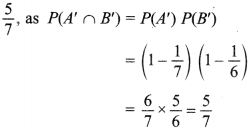
9. Three persons A, B and C, fire a target in turn. Their probabilities of hitting the target are 0.2,0.3 and 0.5 respectively, the probability that target hit is _________ .
Answer:
0.72, as /^target hit)
= P(at least one hits the target)
= 1 – P( none hits) =1 −P(A¯B¯C¯)
10. If A and B are independent events, then P(A and B) = P(A) + P(B). State true or false.
Answer: False, as P(A and B) = P(A) P(B).
11. A speaks truth in 70% cases and B speaks truth in 85% cases. The probability that they speak the same fact is ______ .
Answer:

12. Given P(A) = 0.4, P(B) = 0.7 and P(B/A) = 0.6. Find P(A ∪ B).
Answer:
P(B/A) = P(A∩B)P(A)
⇒ 0.6 × 0.4 = P (A ∩ B)
⇒ P(A ∩ B) = 0.24
Now, P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.4 + 0.7 – 0.24
= 0.86
Class 12 Maths Chapter 13 MCQs
13. Given P(A) = 12 p(B) = 13 and P(A ∩ B) = 16. Are the events A and B independent?
Answer:
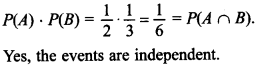
14. Prove that if E and F are independent events, then the events E and F are also independent. [Delhi 2017]
Answer:
As E and F are independent events
∴ P(E ∩ F) = P(E)P(F) …(i)
Consider,
P(E)P(F) = P(E)[1 – P(F)]
= P(E) – P(E)P(F)
= P(E) – P(E ∩ F)
P(E)P(F’) = P(E ∩ F’)
⇒ E and F’ are independent events.
15. A die, whose faces are marked 1, 2, 3 in red and 4,5,6 in green, is tossed. Let A be the event “number obtained is even” and B be the event “number obtained is red”. Find if A and B are independent events. [AI 2017]
Answer:
A : number is even, i.e. 2, 4, 6; P(A) = 36
= 12
B : number is red, i.e. 1, 2, 3; P(B) = 36
= 12
A ∩ B : number is even and red, i.e. 2;
P(A ∩ B) = 16
P(A) × P(B) = 12×12=14
As P(A ∩ B) ≠ P(A) . P(B)
Hence, not independent.
16. A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4. [CBSE 2018]
Answer:
A : sum 8, i.e. (2, 6), (3, 5), (4, 4), (5, 3), (6, 2)
B : red die number less than 4.
B : (1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (6, 2), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3).
A ∩ B : (6, 2), (5, 3)
∴ Conditional probability of obtaining sum 8, given that red die resulted in number less than 4.
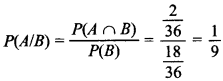
17. 12 cards numbered 1 to 12 are placed in a box, mixed up thoroughly and then a card is drawn at random from the box. If it is known that the number on the drawn card is more than 3, find the probability that it is an even number.
Answer:
Total cards are 12
A : number drawn is more than 3, i.e. 4, 5, 6, …, 12.
B : getting an even number, i.e. 2, 4, 6, 8, 10, 12.
A ∩ B : 4, 6, 8, 10, 12
18. One card is drawn from a well shuffled pack of 52 cards. If E is the event “the card drawn is a king or a queen” and F is the event “the card drawn is an ace or a queen,” then find the probability of the conditional event E/F. [HOTS]
Answer:

19. Two cards are drawn from a well shuffled pack of 52 cards one after the other without replacement. Find the probability that one of them is a queen and the other is a king of opposite colour. Class 12 Maths Chapter 13 MCQs
Answer:

20. A coin is tossed thrice and all eight outcomes are assumed equally likely. Let the event E be “the first throw results in head” and event F be “the last throw results in tail”. Find whether events E and F are independent.
Answer:
Sample space
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
E: first throw results in head = {HHH,HHT,HTH,HTT}
F: Last throw result in tail = {HHT, HTT, THT, TTT}

21. Two dice are thrown. Find the probability that the numbers appeared have a sum 8 if it is known that the second die always exhibits 4. [HOTS]
Answer:
A: Sum of the numbers is 8, i.e. {(2,6), (3,5), (4,4), (5,3), (6,2)}
B: the second die always exhibits 4, i.e. {(1,4), (2,4), (3,4), (4,4), (5,4), (6,4)} A ∩ B= {(4, 4)}
Required probability,
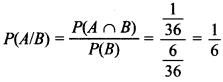
22. If P(A)=0.8,P(B)=0.5 andP(B/A)=0.4, find (i) P(A ∩ B) (ii) P(A/B) (iii) P(A ∪ B). [NCERT]
Answer:
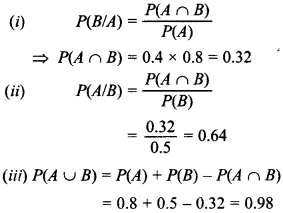
23. The value of k, for which the following distribution is a probability distribution
 Class 12 Maths Chapter 13 MCQs
Class 12 Maths Chapter 13 MCQs
Answer:

24. Find mean (µ) and variance (a2) for the following probability distribution:

Answer:

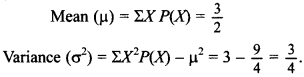
25. A random variable X has a probability distribution P(X) of the following form where k is some number:Determine (i) k (ii) P(X ≤ 2) (iii) P(X ≤ 2) (iv) P(X ≥ 2). [NCERT; Delhi 2019]
Answer:
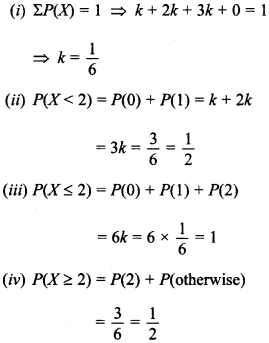
Telegram Class 12 Maths Chapter 13 MCQs
