NCERT Solutions for Class 6 Maths Chapter 2: NCERT Solutions for Class 6 Maths Chapter 2 Whole Numbers Exercise 2.1
- Class 6 Maths Chapter 2 Exercise 2.1
- Class 6 Maths Chapter 2 Exercise 2.2
- Class 6 Maths Chapter 2 Exercise 2.3
NCERT Solutions for Class 6 Maths Chapter 2 Whole Numbers Exercise 2.1
1. Write the next three natural numbers after 10999.
Solution:
Given any natural number, the next number is obtained by adding 1 to the given number.
Therefore, the successors of 10999 are obtained as follows:
10,999 + 1 = 11,000
11,000 + 1 = 11,001
11,001 + 1 = 11,002
Hence, the next three natural numbers after 10999 are 11,000, 11,001 and 11,002.
2. Write the three whole numbers occurring just before 10001.
Solution:
Given any whole number, its predecessor is obtained by subtracting 1 from the given number.
Therefore, the three predecessors of 10001 are obtained as follows:
10,001 − 1 = 10,000
10,000 − 1 = 9,999
9,999 − 1 = 9,998
Hence, the three whole numbers occurring just before 10001 are 10,000, 9,999 and 9,998.
3. Which is the smallest whole number?
Solution:
The set of whole numbers start with Zero.
Therefore, zero (0) is the smallest whole number.
4. How many whole numbers are there between 32 and 53?
Solution:
The count of whole numbers between a and b is given by b − a − 1.
Here, b = 53, a = 32
Hence,
53 − 32 − 1 = 20
Therefore, there are 20 whole numbers between 32 and 53.
5. Write the successor of:
(A)2440701
(B)100199
(C)1099999
(D)2345670
Solution:
The successor of a natural or whole number is obtained by adding 1 to the given number.
(A)Successor of 2440701 is 2440701+1=2440702
(B)Successor of 100199 is 100199+1=100200
(C)Successor of 1099999 is 1099999+1=1100000
(D)Successor of 2345670 is 2345670+1=2345671
6. Write the predecessor of:
(A)94
(B)10000
(C)208090
(D)7654321
Solution:
The predecessor of a number can be obtained by subtracting 1 from the given number.
Therefore,
(A)Predecessor of 94 is 94−1=93
(B)Predecessor of 10000 is 10000−1=9999
(C)Predecessor of 208090 is 208090−1=208089
(D)Predecessor of 7654321 is 7654321−1=7654320
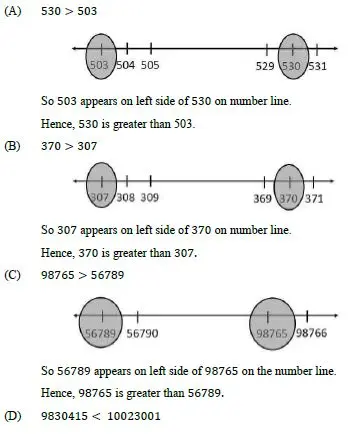
7. In each of the following pairs of numbers, state which whole number is on the left of the other number one the number line? Also write them with the appropriate sign (>,<) between them.
(A) 530,503
(B) 370,307
(C) 98765,56789
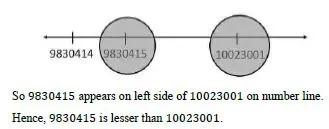
(D) 9830415,10023001
Solution:
Given two whole numbers, the number on the right of the other on the number line is the greater number.
8. Which of the following statements are true (T) and which are false (F):
(a) Zero is the smallest natural number.
(A) True
(B) False
Solution:(B)
Natural number starts from 1.
So, zero is not a part of the natural number set.
Hence, it is false.
(b) 400 is the predecessor of 399.
(A) True
(B) False
Solution:(B)
Predecessor of 399 is obtained by subtracting 1 from 399.
Therefore, predecessor of 399 is: 399−1=398
Hence, it is false.
(c) Zero is the smallest whole number.
(A) True
(B) False
Solution:(A)
The set of whole numbers begin with a zero.
Therefore, zero is the smallest whole number.
Hence, it is true.
(d) 600 is the successor of 599.
(A) True
(B) False
Solution:(A)
The successor of a given number is obtained by adding 1 to the given number.
Therefore, successor of 599 is: 599+1=600
Hence, the given statement is true.
(e) All-natural numbers are whole numbers.
(A) True
(B) False
Solution:(A)
The set of whole numbers consists of all the natural numbers and zero.
Natural numbers are 1,2,3,4,5,…..
Whole numbers are 0,1,2,3,4,5,…..
Since, 1,2,3,4,5,….. is in whole number.
Therefore, all-natural numbers are whole numbers.
Hence, the given statement is true.
(f) All whole numbers are natural numbers.
(A) True
(B) False
Solution:(B)
Natural numbers are 1,2,3,4,5,…..
Whole numbers are 0,1,2,3,4,5,…..
The set of natural numbers does not contain zero.
Hence, the given statement is false.
(g) The predecessor of a two-digit number is never a single digit number.
(A) True
(B) False
Solution:(B)
For example, consider the number 10. Predecessor of 10 is obtained by subtracting 1 from 10.
∴10−1=9
Clearly 10 is a two-digit number while its predecessor 9, is a single digit number.
Hence, the given statement is false.
(h) 1 is the smallest whole number.
(A) True
(B) False
Solution:(B)
The set of whole numbers begin with zero.
Whole numbers are 0,1,2,3,4,5,…..
Hence, zero is the smallest whole number.
Therefore, the given statement is false.
(i) The natural number 1 has no predecessor.
(A) True
(B) False
Solution:(A)
The set of natural numbers start with 1.
Natural numbers are 1,2,3,4,5,…..
Hence the natural number 1 has no predecessor.
Therefore, the given statement is true.
(j) The whole number 1 has no predecessor.
(A) True
(B) False
Solution:(B)
The set of whole numbers begin with zero.
Whole numbers are 0,1,2,3,4,5,…..
Hence zero precedes the whole number one.
Therefore, the given statement is false.
(k) The whole number 13 lies between 11 and 12.
(A) True
(B) False
Solution:(B)
On the number line of whole numbers, we can clearly observe that there exists no whole number between 11 and 12.
So, 13 lies after 11 and 12.
Hence, 13 cannot lie between 11 and 12.
Therefore, the given statement is false.
(l) The whole number 0 has no predecessor.
(A) True
(B) False
Solution:(A)
The set of whole numbers begin with zero.
Hence there exists no number that precedes zero.
Therefore, the given statement is true.
(m) The successor of a two-digit number if always a two digit number.
(A) True
(B) False
Solution:(B)
For example, consider a two-digit number 99.
The successor of 99 is obtained by adding 1 to it.
Therefore, the successor of 99 is:
99+1=100.
Clearly, 99 is a two-digit number while its successor 100, is a three-digit number.
Hence, the given statement is false.
Write the next three natural numbers after 999.
The next three natural numbers after 999 are 1000, 1001 and 1002
