NCERT Solutions Class 12 Maths – Chapter 1 – Relations and Functions: Going through the NCERT solutions is a crucial part of your preparation for Class 12 board exams, JEE (Main and Advanced) and other exams. This will clear your doubts in regards to any question and improve your application skills.
In this article, we will provide you with NCERT Solutions for Class 12 Maths – Chapter 1 – Relations and Functions
NCERT Solutions for Class 12 Maths Chapter 1- Relations and Functions
Class 12 Maths Chapter 1- Relations and Functions :
Top Concepts in Relations
- Introduction to Relation and no. of relations
- A relation R between two non-empty sets A and B is a subset of their Cartesian product A × B.
- If A = B, then the relation R on A is a subset of A × A.
- The total number of relations from a set consisting of m elements to a set consisting of n elements is 2mn.
- If (a, b) belongs to R, then a is related to b and is written as ‘a R b’. If (a, b) does not belong to R, then a is not related to b and it is written as
- Co-domain and Range of a Relation
Let R be a relation from A to B. Then the ‘domain of
- Types of Relations
A relation R in a set A is called an empty relation if no element of A is related to any element of A, i.e.,
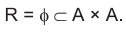
A relation R in a set A is called a universal relation if each element of A is related to every element of A, i.e., R = A × A.
- A relation R on a set A is called:
- Reflexive, if (a, a) R for every a A.
- Symmetric, if (a1, a2) R implies that (a2, a1) R for all a1, a2 ∈ A.
- Transitive, if (a1, a2) R and (a2, a3) R implies that (a1, a3) R for all a1, a2, a3 ∈ A.
- Equivalence Relation
- A relation R in a set A is said to be an equivalence relation if R is reflexive, symmetric and transitive.
- An empty relation R on a non-empty set X (i.e., ‘a R b’ is never true) is not an equivalence relation, because although it is vacuously symmetric and transitive, but it is not reflexive (except when X is also empty).
- Given an arbitrary equivalence relation R in a set X, R divides X into mutually disjoint subsets Si called partitions or subdivisions of X provided:
- All elements of S, are related to each other for all i.
- No element of Si is related to any element of St if i j.
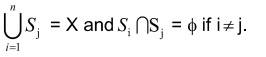
The subsets St are called equivalence classes.
- Union, Intersection and Inverse of Equivalence Relations
- If R and S are two equivalence relations on a set A, R S is also an equivalence relation on A.
- The union of two equivalence relations on a set is not necessarily an equivalence relation on the set.
- The inverse of an equivalence relation is an equivalence relation.
Top Concepts in Functions
- Introduction to functions
A function from a non-empty set A to another non-empty set B is a correspondence or a rule which associates every element of A to a unique element of B written as f : A → B such that f(x) = y for all x A, y B.
All functions are relations, but the converse is not true.
- Domain, Co-domain and Range of a Function
- If f : A → B is a function, then set A is the domain, set B is the co-domain and set {f(x) : x A) is the range of f.
- The range is a subset of the co-domain.
- A function can also be regarded as a machine which gives a unique output in set B corresponding to each input from set A.
- If A and B are two sets having m and n elements, respectively, then the total number of functions from A to B is nm.
- Real Function
- A function f : A → B is called a real-valued function if B is a subset of R.
- If A and B both are subsets of R, then ‘f’ is called a real function.
- While describing real functions using mathematical formula, x (the input) is the independent variable and y (the output) is the dependent variable.
- The graph of a real function ‘f’ consists of points whose co-ordinates (x, y) satisfy y = f(x), for all x Domain(f).
- Vertical line test
A curve in a plane represents the graph of a real function if and only if no vertical line intersects it more than once.
- One–one Function
- A function f : A → B is one-to-one if for all x, y A, f(x) = f(y) ⇒ x = y or x ≠ y ⇒ f(x) ≠ f(y).
- A one-one function is known as an injection or injective function. Otherwise, f is called many-one.
- Onto Function
- A function f : A → B is an onto function, if for each b B, there is at least one a A such that f(a) = b, i.e., if every element in B is the image of some element in A, then f is an onto or surjective function.
- For an onto function, range = co-domain.
- A function which is both one-one and onto is called a bijective function or a bijection.
- A one-one function defined from a finite set to itself is always onto, but if the set is infinite, then it is not the case.
- Let A and B be two finite sets and f : A → B be a function.
- If f is an injection, then n (A) n (B) .
- If f is a surjection, then n(A) n(B).
- If f is a bijection, then n(A) = n(B) .
- If A and B are two non-empty finite sets containing m and n elements, respectively, then Number of functions from A to B = nm.
- Number of one-one function from A to B
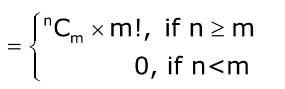
- Number of onto functions from A to B
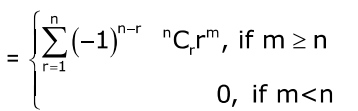
- Number of one-one and onto functions from A to B
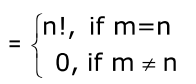
- If a function f : A → B is not an onto function, then f : A → f(A) is always an onto function.
- Composition of Functions
Let f : A → B and g : B → C be two functions. The composition of f and g, denoted by g o f, is defined as the function g o f: A → C and is given by g o f(x): A → C defined by g o f(x) = g(f(x)) ∀ x∈ A.
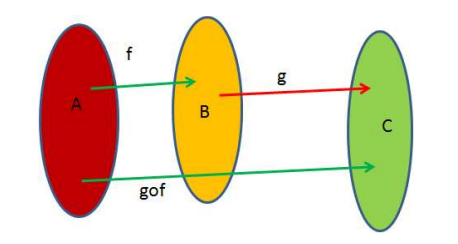
- Composition of f and g is written as g o f and not f o g.
- g o f is defined if the range of f
domain of g, and f o g is defined if the range of g
domain of f.
- Composition of functions is not commutative in general i.e., f o g(x) ≠ g o f(x).
- Composition is associative i.e., if f : X → Y, g : Y → Z and h : Z → S are functions, then h o (g o f) = (h o g) o f.
- The composition of two bijections is a bijection.
- Inverse of a Function
- Let f : A → B is a bijection, then g : B → A is inverse of f if f(x) = y ⟺ g(y) = x OR g o f = lA and f o g = lB
- If g o f = lA and f is an injection, then g is a surjection.
- If f o g’ lB and f is a surjection, then g is an injection.
- Let f : A → B and g: B → C be two functions. Then
- g o f: A → C is onto ⇒ g: B → C is onto.
- g o f: A → C is one-one ⇒ f:A → B is one-one.
- g o f: A → C is onto and g: B → C is one-one ⇒ f:A → B is onto.
- g o f: A → C is one-one and f:A → B is onto ⇒ g: B → C is one-one.
- Invertible Function
- A function f : X → Y is defined to be invertible if there exists a function g : Y → X such that gof – lx and fog = Iy.
- The function g is called the inverse of f and is denoted by f-1. If f is invertible, then f must be one-one and onto, and conversely, if f is one-one and onto, then f must be invertible.
- If f : A → B and g : B → C are one-one and onto, then g o f : A → C is also one-one and onto. But if g o f is one-one, then only f is one-one and g may or may not be one-one. If g o f is onto, then g is onto and f may or may not be onto.
- Let f : X → Y and g : Y → Z be two invertible functions. Then g o f is also invertible with (g o f)-1 = f-1 o g-1.
- If f: R → R is invertible, f(x) = y, then f-1 (y) = x and (f-1)-1 is the function f itself.
Binary Operations
- A binary operation * on a set A is a function from A × A to A.
- If * is a binary operation on a set S, then S is closed with respect to *.
- Binary operations on R
- Addition, subtraction and multiplication are binary operations on R, which is the set of real numbers.
- Division is not binary on R; however, division is a binary operation on R – {0} which is the set of non-zero real numbers.
- Laws of Binary Operations
- A binary operation * on the set X is called commutative, if a * b = b * a, for every a, b X.
- A binary operation * on the set X is called associative, if a (b*c) = (a*b)*c, for every a, b, c X.
- An element e A is called an identity of A with respect to * if for each a A, a * e = a = e * a.
- The identity element of (A, *) if it exists, is unique.
- Existence of Inverse
Given a binary operation * from A × A → A with the identity element e in A, an element a e A is said to be invertible with respect to the operation *, if there exists an element b in A such that a * b = e = b * a and b is called the inverse of a and is denoted by a-1.
- If the operation table is symmetric about the diagonal line, then the operation is commutative.
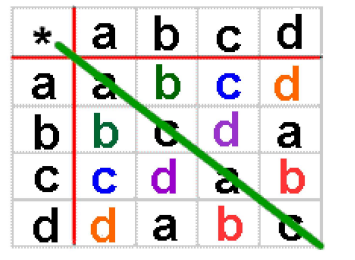
The operation * is commutative.
- Binary Operation on Natural Numbers
Addition ’+’ and multiplication ‘-‘ on N, the set of natural numbers, are binary operations. However, subtraction ‘—’ and division are not, because (4, 5) = 4 – 5 = -1 N and 4/5 = .8 N.
- Number of Binary Operations
- Let S be a finite set consisting of n elements. Then S x S has n2 elements.
- The total number of functions from a finite set A to a finite set B is [n(B)]n(A). Therefore, total number of binary operations on S is nn2.
- The total number of commutative binary operations on a set consisting of n elements is n n(n-1)2.
Important Questions
Multiple Choice questions-
- Let R be the relation in the set (1, 2, 3, 4}, given by:
R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}.
Then:
(a) R is reflexive and symmetric but not transitive
(b) R is reflexive and transitive but not symmetric
(c) R is symmetric and transitive but not reflexive
(d) R is an equivalence relation.
2. Let R be the relation in the set N given by: R = {(a, b): a = b – 2, b > 6}. Then:
(a) (2, 4) ∈ R
(b) (3, 8) ∈ R
(c) (6, 8) ∈ R
(d) (8, 7) ∈ R.
3. Let A = {1, 2, 3}. Then number of relations containing {1, 2} and {1, 3}, which are reflexive and symmetric but not transitive is:
(a) 1
(b) 2
(c) 3
(d) 4.
4. Let A = (1, 2, 3). Then the number of equivalence relations containing (1, 2) is
(a) 1
(b) 2
(c) 3
(d) 4.
5. Let f: R → R be defined as f(x) = x4. Then
(a) f is one-one onto
(b) f is many-one onto
(c) f is one-one but not onto
(d) f is neither one-one nor onto.
6. Let f: R → R be defined as f(x) = 3x. Then
(a) f is one-one onto
(b) f is many-one onto
(c) f is one-one but not onto
(d) f is neither one-one nor onto.
7. If f: R → R be given by f(x) = (3 – x³)1/3, then fof (x) is
(a) x1/3
(b) x³
(c) x
(d) 3 – x³.
8. Let f: R – {- 43} → R be a function defined as: f(x) = 4x3x + 4, x ≠ – 43. The inverse of f is map g: Range f → R -{- 43} given by
(a) g(y) = 3y3- 4y
(b) g(y) = 4y4 – 3y
(c) g(y) = 4y3 – 4y
(d) g(y) = 3y4 – 3y
9. Let R be a relation on the set N of natural numbers defined by nRm if n divides m. Then R is
(a) Reflexive and symmetric
(b) Transitive and symmetric
(c) Equivalence
(d) Reflexive, transitive but not symmetric.
10. Set A has 3 elements, and the set B has 4 elements. Then the number of injective mappings that can be defined from A to B is:
(a) 144
(b) 12
(c) 24
(d) 64
Answer Key-Multiple Choice Questions–
(b) R is reflexive and transitive but not symmetric
(c) (6, 8) ∈ R
(a) 1
(b) 2
(d) f is neither one-one nor onto.
(a) f is one-one onto
(c) x
(b) g(y) = 4y4 – 3y
(b) Transitive and symmetric
(c) 24
Very Short Questions:
- If R = {(x, y) : x + 2y = 8} is a relation in N, write the range of R.
- Show that a one-one function:
f {1, 2, 3} → {1, 2, 3} must be onto. (N.C.E.R.T.)
- What is the range of the function f(x) = |x – 1|x – 1 ? (C.B.S.E. 2010)
- Show that the function f : N → N given by f(x) = 2x is one-one but not onto. (N.C.E.R.T.)
- If f : R → R is defined by f(x) = 3x + 2 find f(f(x)). C.B.S.E. 2011 (F))
- If f(x) = xx – 1, x ≠1 then find fof. (N.C.E.R.T)
- If f: R → R is defined by f(x) = (3 – x3)1/3, find fof (x)
- Are f and q both necessarily onto, if gof is onto? (N.C.E.R.T.)
Very Short Answer:
- Solution: Range of R = {1, 2, 3}.
[∵ When x = 2, then y = 3, when x = 4, then y = 2, when x = 6, then y = 1]
- Solution: Since ‘f’ is one-one,
∴ under ‘f’, all the three elements of {1, 2, 3} should correspond to three different elements of the co-domain {1, 2, 3}.
Hence, ‘f’ is onto.
- Solution: When x > 1,
than f(x) = x – 1x – 1 = 1.
When x < 1,
than f(x) = -(x – 1)x – 1 = -1
Hence, Rf = {-1, 1}.
- Solution:
Let x1, x2 ∈ N.
Now, f(x1) = f(x2)
⇒ 2x1 = 2x2
⇒ x1 = x2
⇒ f is one-one.
Now, f is not onto.
∵ For 1 ∈ N, there does not exist any x ∈ N such that f(x) = 2x = 1.
Hence, f is ono-one but not onto.
- Solution:
f(f(x)) = 3 f(x) + 2
= 3(3x + 2) + 2 = 9x + 8.
- Solution:
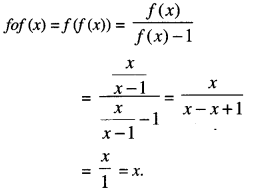
- Solution:
fof(x) = f(f(x)) = (3-(f(x))3)1/3
= (3 – ((3 – x3)1/3)3)1/3
= (3 – (3 – x3))1/3 = (x3)1/3 = x.
- Solution:
Consider f: {1, 2, 3, 4} → {1, 2, 3, 4}
and g: {1, 2, 3,4} → {1,2.3} defined by:
f(1) = 1, f(2) = 2, f(3) = f(4) = 3
g (1) = 1, g (2) = 2, g (3) = g (4) = 3.
∴ gof = g (f(x)) {1, 2,3}, which is onto
But f is not onto.
[∵ 4 is not the image of any element]
Short Questions:
- Let A be the set of all students of a Boys’ school. Show that the relation R in A given by:
R = {(a, b): a is sister of b} is an empty relation and the relation R’ given by :
R’ = {(a, b) : the difference between heights of a and b is less than 3 metres} is an universal relation. (N.C.E.R.T.)
- Solution:
(i) Here R = {(a, b): a is sister of b}.
Since the school is a Boys’ school,
∴ no student of the school can be the sister of any student of the school.
Thus R = Φ Hence, R is an empty relation.
(ii) Here R’ = {(a,b): the difference between heights of a and b is less than 3 metres}.
Since the difference between heights of any two students of the school is to be less than 3 metres,
∴ R’ = A x A. Hence, R’ is a universal relation.
- Let f : X → Y be a function. Define a relation R in X given by :
R = {(a,b):f(a) = f(b)}.
Examine, if R is an equivalence relation. (N.C.E.R.T.)
- Solution:
For each a ∈ X, (a, a) ∈ R.
Thus R is reflexive. [∵ f (a) = f(a)]
Now (a, b) ∈ R
⇒ f(a) = f(b)
⇒ f(b) = f (a)
⇒ (b, a) ∈ R.
Thus R is symmetric.
And (a, b) ∈ R
and (b, c) ∈ R
⇒ f(a) = f(b)
and f(b) = f(c)
⇒ f(a)= f(c)
⇒ (a, c) ∈ R.
Thus R is transitive.
Hence, R is an equivalence relation.
- Let R be the relation in the set Z of integers given by:
R = {(a, b): 2 divides a – b}.
Show that the relation R is transitive. Write the equivalence class [0]. (C.B.S.E. Sample Paper 2019-20)
- Solution:
Let 2 divide (a – b) and 2 divide (b – c), where a,b,c ∈ Z
⇒ 2 divides [(a – b) + (b – c)]
⇒ 2 divides (a – c).
Hence, R is transitive.
And [0] = {0, ± 2, ± 4, ± 6,…].
- Show that the function:
f : N → N
given by f(1) = f(2) = 1 and f(x) = x -1, for every x > 2 is onto but not one-one. (N.C.E.R.T.)
- Solution:
Since f(1) = f(2) = 1,
∴ f(1) = f(2), where 1 ≠ 2.
∴ ‘f’ is not one-one.
Let y ∈ N, y ≠ 1,
we can choose x as y + 1 such that f(x) = x – 1
= y + 1 – 1 = y.
Also 1 ∈ N, f(1) = 1.
Thus ‘f ’ is onto.
Hence, ‘f ’ is onto but not one-one.
- Find gof and fog, if:
f : R → R and g : R → R are given by f (x) = cos x and g (x) = 3x2. Show that gof ≠ fog. (N. C.E.R. T.)
- Solution:
We have:
f(x) = cos x and g(x) = 3x2.
∴ gof (x) = g (f(x)) = g (cos x)
= 3 (cos x)2 = 3 cos2 x
and fog (x) = f(g (x)) = f(3x2) = cos 3x2.
Hence, gof ≠ fog.
- If f(x) = 4x + 36x – 4, x ≠ 23 find fof(x)
- Solution:
We have: 4x + 36x – 4 …(1)
∴ fof(x) – f (f (x))
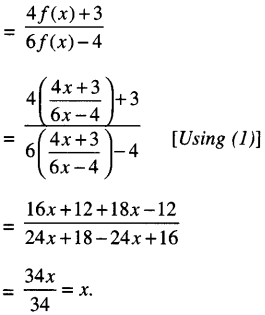
- Let A = N x N be the set of ail ordered pairs of natural numbers and R be the relation on the set A defined by (a, b) R (c, d) iff ad = bc. Show that R is an equivalence relation.
- Solution:
Given: (a, b) R (c, d) if and only if ad = bc.
(I) (a, b) R (a, b) iff ab – ba, which is true.
[∵ ab = ba ∀ a, b ∈ N]
Thus, R is reflexive.
(II) (a, b) R (c,d) ⇒ ad = bc
(c, d) R (a, b) ⇒ cb = da.
But cb = be and da = ad in N.
∴ (a, b) R (c, d) ⇒ (c, d) R (a, b).
Thus, R is symmetric.
(III) (a,b) R (c, d)
⇒ ad = bc …(1)
(c, d) R (e,f)
⇒ cf = de … (2)
Multiplying (1) and (2), (ad). (cf) – (be), (de)
⇒ af = be
⇒ (a,b) = R(e,f).
Thus, R is transitive.
Thus, R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation.
- Let f: R → R be the Signum function defined as:
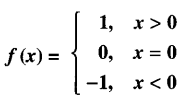
and g : R → R be the Greatest Integer Function given by g (x) = [x], where [x] is greatest integer less than or equal to x. Then does fog and gof coincide in (0,1]?
- Solution:
For x ∈ (0,1].
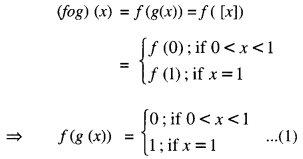
And (gof) (x) = g(f(x)) = g(1)
[∵ f(x) = 1 ∀ x > 0]
= [1] = 1
⇒ (gof) (x) = 1 ∀ x ∈ (0, 1] …(2)
From (1) and (2), (fog) and (gof) do not coincide in (0, 1].
Long Questions / Answer:
- Show that the relation R on R defined as R = {(a, b):a ≤ b}, is reflexive and transitive but not symmetric.
- Solution:
We have: R = {(a, b)} = a ≤ b}.
Since, a ≤ a ∀ a ∈ R,
∴ (a, a) ∈ R,
Thus, R reflexive.
Now, (a, b) ∈ R and (b, c) ∈ R
⇒ a ≤ b and b ≤ c
⇒ a ≤ c
⇒ (a, c) ∈ R.
Thus, R is transitive.
But R is not symmetric
[∵ (3, 5) ∈ R but (5, 3) ∉ R as 3 ≤ 5 but 5 > 3]
Solution:
Let x1, x2 ∈ N.
Now, f(x1) = f(x2)
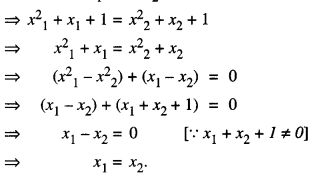
Thus, f is one-one.
Let y ∈ N, then for any x,
f(x) = y if y = x2 + x + 1
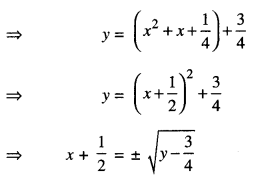
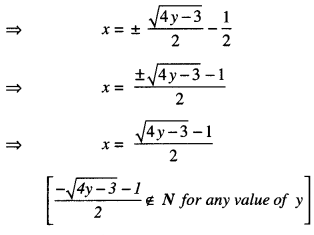

- Prove that function f : N → N, defined by f(x) = x2 + x + 1 is one-one but not onto. Find inverse of f : N → S, where S is range of f.
- Solution:
We have:
R = {(a, b): a, b ∈ A; |a – b| is divisible by 4}.
(1) Reflexive: For any a ∈ A,
∴ (a, b) ∈ R.
|a – a| = 0, which is divisible by 4.
Thus, R is reflexive.
Symmetric:
Let (a, b) ∈ R
⇒ |a – b| is divisible by 4
⇒ |b – a| is divisible by 4
Thus, R is symmetric.
Transitive: Let (a, b) ∈ R and (b, c) ∈ R
⇒ |a – b| is divisible by 4 and |b – c| is divisible by 4
⇒ |a – b| = 4λ
⇒ a – b = ±4λ ………….(1)
and |b – c| = 4µ
⇒ b – c = ± 4µ ………….(2)
Adding (1) and (2),
(a-b) + (b-c) = ±4(λ + µ)
⇒ a – c = ± 4 (λ + µ)
⇒ (a, c) ∈ R.
Thus, R is transitive.
Now, R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation.
(ii) Let ‘x’ be an element of A such that (x, 1) ∈ R
⇒ |x – 1| is divisible by 4
⇒ x – 1 = 0,4, 8, 12,…
⇒ x = 1, 5, 9, 13, …
Hence, the set of all elements of A which are related to 1 is {1, 5, 9}.
(iii) Let (x, 2) ∈ R.
Thus |x – 2| = 4k, where k ≤ 3.
∴ x = 2, 6, 10.
Hence, equivalence class [2] = {2, 6, 10}.
- Let A = (x ∈Z : 0 ≤ x ≤ 12}.
Show that R = {(a, b) : a, b ∈ A; |a – b| is divisible by 4} is an equivalence relation. Find the set of all elements related to 1. Also write the equivalence class [2]. (C.B.S.E 2018)
- Solution:
Let y∈ R.
For any x, f(x) = y if y = 9x2 + 6x – 5
⇒ y = (9x2 + 6x + 1) – 6
= (3x + 1)2 – 6
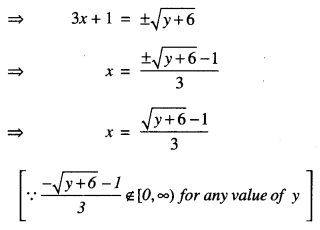

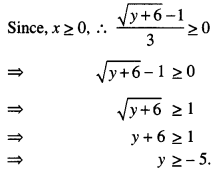

- Prove that the function f: [0, ∞) → R given by f(x) = 9x2 + 6x – 5 is not invertible. Modify the co-domain of the function f to make it invertible, and hence find f-1. (C.B.S.E. Sample Paper 2018-19
Assertion and Reason Questions-
1. Two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes(a), (b), (c) and (d) as given below.
- Both A and R are true and R is the correct explanation of A.
- Both A and R are true but R is not the correct explanation of A.
- A is true but R is false.
- A is false and R is also false.
Assertion(A): Let L be the set of all lines in a plane and R be the relation in L defined as R = {(L1, L2): L1 is perpendicular to L2}.R is not equivalence realtion.
Reason (R): R is symmetric but neither reflexive nor transitive
Answer: 1. (a)Both A and R are true and R is the correct explanation of A.
2. Two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes(a), (b), (c) and (d) as given below.
- Both A and R are true and R is the correct explanation of A.
- Both A and R are true but R is not the correct explanation of A.
- A is true but R is false.
- A is false and R is also false.
Assertion (A): = {(T1, T2): T1 is congruent to T2}. Then R is an equivalence relation.
Reason(R): Any relation R is an equivalence relation, if it is reflexive, symmetric and transitive.
Answer: 2. (a) Both A and R are true and R is the correct explanation of A.
Case Study Questions
1. Consider the mapping f: A → B is defined by f(x) = x – 1 such that f is a bijection.
Based on the above information, answer the following questions.
- Domain of f is:
- R – {2}
- R
- R – {1, 2}
- R – {0}
- Range of f is:
- R
- R – {2}
- R – {0}
- R – {1, 2}
- If g: R – {2} → R – {1} is defined by g(x) = 2f(x) – 1, then g(x) in terms of x is:
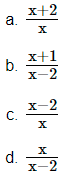
- The function g defined above, is:
- One-one
- Many-one
- into
- None of these
- A function f(x) is said to be one-one if.
- f(x1) = f(x2) ⇒ -x1 = x2
- f(-x1) = f(-x2) ⇒ -x1 = x2
- f(x1) = f(x2) ⇒ x1 = x2
- None of these
2. A relation R on a set A is said to be an equivalence relation on A iff it is:
- Reflexive i.e., (a, a) ∈ R ∀ a ∈ A.
- Symmetric i.e., (a, b) ∈ R ⇒ (b, a) ∈ R ∀ a, b ∈ A.
- Transitive i.e., (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R ∀ a, b, c ∈ A.
Based on the above information, answer the following questions.
- If the relation R = {(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)} defined on the set A = {1, 2, 3}, then R is:
- Reflexive
- Symmetric
- Transitive
- Equivalence
- If the relation R = {(1, 2), (2, 1), (1, 3), (3, 1)} defined on the set A = {1, 2, 3}, then R is:
- Reflexive
- Symmetric
- Transitive
- Equivalence
- If the relation R on the set N of all natural numbers defined as R = {(x, y): y = x + 5 and x < 4}, then R is:
- Reflexive
- Symmetric
- Transitive
- Equivalence
- If the relation R on the set A = {1, 2, 3, ………, 13, 14} defined as R = {(x, y): 3x – y = O}, then R is:
- Reflexive
- Symmetric
- Transitive
- Equivalence
- If the relation R on the set A = {I, 2, 3} defined as R = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}, then R is:
- Reflexive only
- Symmetric only
- Transitive only
- Equivalence
Case Study Answers-
1. Answer :
- (a) R – {2}
Solution:
For f(x) to be defined x – 2; ≠ 0 i.e., x; ≠ 2.
∴ Domain of f = R – {2}
- (b) R – {2}
Solution:
Let y = f(x), then
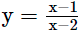
⇒ xy – 2y = x – 1 ⇒ xy – x = 2y –
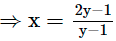
Since, x ∈∈ R – {2}, therefore y ≠ 1
Hence, range of f = R – {1}
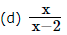
Solution:
We have, g(x) = 2f(x) – 1
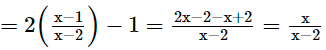
- (a) One-one
Solution:
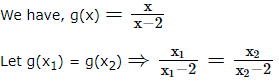
⇒ x1x2 – 2x1 = x1x2 – 2x2 ⇒ 2x1 = 2x2 ⇒ x1 = x2
Thus, g(x1) = g(x2) ⇒ x1 = x2
Hence, g(x) is one-one.
- (c) f(x1) = f(x2) ⇒ x1 = x2
2. Answer :
- (a) Reflexive
Solution:
Clearly, (1, 1), (2, 2), (3, 3), ∈ R. So, R is reflexive on A.
Since, (1, 2) ∈ R but (2, 1) ∉ R. So, R is not symmetric on A.
Since, (2, 3), ∈ R and (3, 1) ∈ R but (2, 1) ∉ R. So, R is not transitive on A.
- (b) Symmetric
Solution:
Since, (1, 1), (2, 2) and (3, 3) are not in R. So, R is not reflexive on A.
Now, (1, 2) ∈ R ⇒ (2, 1) ∈ R and (1, 3) ∈ R ⇒ (3, 1) ∈ R. So, R is symmetric,
Clearly, (1, 2) ∈ R and (2, 1) ∈ R but (1, 1) ∉ R. So, R is not transitive on A.
- (c) Transitive
Solution:
We have, R = {(x, y): y = x + 5 and x < 4}, where x, y ∈ N.
∴ R = {(1, 6), (2, 7), (3, 8)}
Clearly, (1, 1), (2, 2) etc. are not in R. So, R is not reflexive.
Since, (1, 6) ∈ R but (6, 1) ∉ R. So, R is not symmetric.
Since, (1, 6) ∈ R and there is no order pair in R which has 6 as the first element.
Same is the case for (2, 7) and (3, 8). So, R is transitive.
- (d) Equivalence
Solution:
We have, R = {(x, y): 3x – y = 0}, where x, y ∈ A = {1,2, ……, 14}.
∴ R = {(1, 3), (2, 6), (3, 9), (4, 12)}
Clearly, (1, 1) ∉ R. So, R is not reflexive on A.
Since, (1, 3) ∈ R but (3, 1) ∉ R. So, R is not symmetric on A.
Since, (1, 3) ∈ Rand (3, 9) ∈ R but (1, 9) ∉ R. So, R is not transitive on A.
- (d) Equi0076alence
Solution:
Clearly, (1, 1), (2, 2), (3, 3) ∈ R. So, R is reflexive on A.
We find that the ordered pairs obtained by interchanging the components of ordered pairs in R are also in R. So, R is symmetric on A. For 1, 2, 3 ∈ A such that (1, 2) and (2, 3) are in R implies that (1, 3) is also, in R. So, R is transitive on A. Thus, R is an equivalence relation.
Class 12 Maths All Chapter Solutions
Key words
class 12 maths ncert solutions, ncert solutions maths class 12, class 12 maths solutions, ncert class 12 maths, ncert class 12 maths solutions, class 12 maths, ncert solutions for class 12 maths, ncert maths class 12 solutions, ncert maths class 12, maths ncert solutions class 12, class 12 maths ncert book, maths deleted syllabus class 12, maths syllabus class 12, maths class 12, maths class 12 ncert solutions, class 10 maths chapter 12, class 10 maths ch 12, maths class 12 syllabus, class 12 maths chapter 1, class 12 maths chapters, ncert solutions for class 12 maths chapter 7, class 12 maths ncert, ncert solutions for class 12 maths chapter 5, maths solutions class 12, ncert maths solutions class 12, ncert solutions class 12 maths, class 12 maths ncert solutions pdf, chapter 6 maths class 12, ncert solutions for class 12 maths chapter 1, class 12 maths ncert pdf, sample paper class 12 maths, maths sample paper class 12 2021, maths sample paper class 12, ncert class 12 maths book pdf, exercise 3.2 class 12 maths, exercise 1.1 class 12 maths, maths class 12 ncert pdf, class 12 maths book, ncert solutions for class 10 maths chapter 12, class 12 maths chapter 3, ncert maths class 12 pdf, syllabus of maths class 12 cbse 2020-21, ncert solution of maths class 12, ncert exemplar class 12 maths, ncert maths class 12 pdf free download, ncert solutions for class 12 maths chapter 4, class 8 maths chapter 12, class 12 maths ncert book pdf, cbse class 12 maths syllabus

