An equation has many forms of slope intercept is one of them is the equation of line slope intercept form contains information about these properties.

The slope-intercept form is a fundamental equation format in algebra, expressed as y = mx + b. It represents a linear relationship between variables, with “m” representing the slope and “b” the y-intercept. This form allows easy graphing, interpretation of slopes, and identification of starting points on the y-axis.

In this article, we will discuss the slope-intercept form concept, the equation of straight-line slope intercept form, the concept of b using the equation of the straight line, and the Application. Also, explain the topic with the help of examples.

Class 10 Maths Formula all Chapters PDF Download

Equation of Straight line: Slope intercept form

Any equation of this form is called the equation of line slope intercept form

If any equation has given two points like (x₁, x₂) and (y₁, y₂), we want to find the slope of line m we can easily find the slope (m) for the following formula

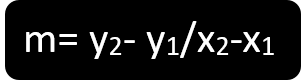
Concept of b

In any line, b is the point where the line crosses the y-axis. Here we give the concept the point b in with the help of a graph

In this graph, the red dot shows the basic characteristic of the y-intercept. Furthermore, red dots are always present on the Cartesian plane’s primary vertical axis.

Standard equation: Derivation of slope intercept form

To derive the slope-intercept form from the standard equation of a line, we start with the general equation for a line:

We follow the following step for derivation 

Step 1: Find “y” on one side.

To convert the standard equation to slope-intercept form, we need to solve for “y.” To do this, subtract “Ax” from both sides of the equation:
Ax + By – Ax = C – Ax
This simplifies to:
By = -Ax + C

Step 2: Solve for “y.”

Now, to isolate “y,” we divide both sides of the equation by “B”:
y = (-A/B) x + C/B

Step 3: show the equation in slope intercept form

In the slope-intercept form (y = mx + b), “m” represents the slope, and “b” represents the y-intercept. Comparing the equation, we obtained in Step 2 with the slope-intercept form; we can identify the slope and y-intercept:
Slope (m) = -A/B
Y-intercept (b) = C/B
Therefore, the slope-intercept form of the line in terms of “m” and “b” is:
y = mx + b
Where “m” is the slope and “b” is the y-intercept, as derived from the standard equation of the line.

Examples of Slope Intercept Form

Example 1: Slope (m)=1/2 and y-intercept of (0,3) Examine the equation of the line

Solution 

Step 1:

Putt gave value to the slope-intercept formula Here, the y-intercept is (0,3), b=3, and also in the given question slope given is (1/2) Put all given values in the slope-intercept formula 

y= (1/2) x +3
½ x – y= -1                                        (1)

The standard form of the equation is newer and written in fraction form so,
Multiply equation one with two on both sides 

2(1/2(x -y)) =2(-1)
x-2y=-2

Example 2:

The slope of 5 and through the point of the axis is (1/3, 5/3)

Solution 

Given data 

Slope (m) = 5

Points 

Step 1:

Put the given data in the point-slope formula

5/3=5(1/2) +b                      (1)

Step 2:

In this step, we find the value of b

Subtract on -5/2 equation one on both sides

5/3 – 5/2= b

After simplification answer is 

b= -5/6

Step 2:

Again, put all values in the original formula of slope intercept form and for this, we find the equation of line

Y =mx + b

Y =5x + (-5/6)

y = 5x – 5/6

To avoid manual calculations of slope intercept form equations, you can try a slope intercept form calculator. 

FAQs

Summary

In this article, we have discussed the slope intercept form concept; intercept form the equation of straight-line slope, the concept of b using the equation of the straight line, and the Application. Also, explain the topic with the help of examples. After briefly studying this article, anyone can defend this topic easily.