Class 12 Maths MCQs With Answers Chapter 1 Relations And Functions

Class 12 Maths MCQs with Answers Chapter 1 Relations and Functions

Page Contents

1. Let R be a relation on the set L of lines defined by l₁ R l₂ if l₁ is perpendicular to l₂, then relation R is
(a) reflexive and symmetric
(b) symmetric and transitive
(c) equivalence relation
(d) symmetric
Answer: d

2. Given triangles with sides T₁ : 3, 4, 5; T₂ : 5, 12, 13; T₃ : 6, 8, 10; T₄ : 4, 7, 9 and a relation R in set of triangles defined as R = {(Δ₁, Δ₂) : Δ₁ is similar to Δ₂}. Which triangles belong to the same equivalence class?
(a) T₁ and T₂
(b) T₂ and T₃
(c) T₁ and T₃
(d) T₁ and T₄
Answer: c

3. Given set A ={1, 2, 3} and a relation R = {(1, 2), (2, 1)}, the relation R will be
(a) reflexive if (1, 1) is added
(b) symmetric if (2, 3) is added
(c) transitive if (1, 1) is added
(d) symmetric if (3, 2) is added
Answer: c

4. Given set A = {a, b, c). An identity relation in set A is
(a) R = {(a, b), (a, c)}
(b) R = {(a, a), (b, b), (c, c)}
(c) R = {(a, a), (b, b), (c, c), (a, c)}
(d) R= {(c, a), (b, a), (a, a)}
Answer: b

5. A relation S in the set of real numbers is defined as xSy ⇒ x – y+ √3 is an irrational number, then relation S is
(a) reflexive
(b) reflexive and symmetric
(c) transitive
(d) symmetric and transitive
Answer: a

[sc name=”article2″ ]

6. Set A has 3 elements and the set B has 4 elements. Then the number of injective functions that can be defined from set A to set B is
(a) 144
(b) 12
(c) 24
(d) 64
Answer: c

7. Given a function lf as f(x) = 5x + 4, x ∈ R. If g : R → R is inverse of function ‘f then
(a) g(x) = 4x + 5
(b) g(x) = 54x−5
(c) g(x) = x−45
(d) g(x) = 5x – 4
Answer: c

8. Let Z be the set of integers and R be a relation defined in Z such that aRb if (a – b) is divisible by 5. Then R partitions the set Z into ______ pairwise disjoint subsets.
Answer: Five

9. Consider set A = {1, 2, 3 } and the relation R= {(1, 2)}, then? is a transitive relation. State true or false.
Answer: True

10. Every relation which is symmetric and transitive is reflexive also. State true or false.
Answer: False

11. Let R be a relation in set N, given by R = {(a, b): a = b – 2, b > 6} then (3, 8) ∈ R. State true or false with reason.
Answer: False

12. Let R be a relation defined as R = {(x, x), (y, y), (z, z), (x, z)} in set A = {x, y, z} then R is (reflexive/symmetric) relation.
Answer: Reflexive, as for all a ∈ A, (a, a) ∈ R.

13. Let R be a relation in the set of natural numbers N defined by R = {(a, b) ∈ N × N: a < b}. Is relation R reflexive? Give a reason.
Answer:
Given R = {(a, b) ∈ N × N: a < b}.
Not reflexive, as for (a, a) × R
⇒ a< a, not true.

14. Let A be any non-empty set and P(A) be the power set of A. A relation R defined on P(A) by X R Y ⇔ X ∩ Y = X, X, Y ∈ P(A). Examine whether is symmetric.
Answer:
X R Y ⇔ X ∩ Y = X ⇒ Y ∩ X = X ⇒ Y R X.
Hence, symmetric.

15. State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive. [NCERT; Delhi 2011]
Answer:
(1, 2) ∈ R, (2, 1) ∈ R, but (1, 1) ∉ R.

16. Show that the relation R in the set {1,2,3} given by R = {(1,1), (2, 2), (3, 3), (1, 2), (2, 3)} is reflexive but neither symmetric nor transitive. [NGERT]
Answer:
Given R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} defined on R: {1, 2, 3} → {1, 2, 3}
For reflexive: As (1, 1), (2,2), (3, 3) ∈ R. Hence, reflexive
For symmetric: (1, 2) ∈ R but (2, 1) ∉ R. Hence, not symmetric.
For transitive: (1, 2) ∈ R and (2, 3) ∈R but (1, 3) ∉ R. Hence, not transitive.

17. Let A = {3, 4, 5} and relation R on set A is defined as R = {(a, b) e A x A : a – b – 10). Is relation an empty relation?
Answer:
We notice for no value of a, b s A, a-b = 10. Hence, (a, b) £ R for a, b e A. Hence, empty relation.

18. Given set A = {a, b} and relation R on A is defined as R = {(a, a), (b, b)}. Is relation an identity relation?
Answer: Yes, as (a, a) ∈ R, for all a ∈ A..

19. Let set A represents the set of all the girls of a particular class. Relation R on A is defined as R = {(a, b) ∈ A × A : difference between weights of a and b is less than 30 kg}. Show that relation R is a universal relation.
Answer:
Let a, b ∈ A then a – b < 30 kg, always true for students of a particular class, i.e. aRb ∀ a, b ∈ A. Hence, universal relation.

20. If A = {1, 2, 3} and relation R = {(2, 3)} in A. Check whether relation R is reflexive, symmetric and transitive.
Answer:
Not reflexive, as (1, 1) ∉ R.
Not symmetric, as (2, 3) ∈ R but (3,2) ∉ R.
Transitive, as relation R in a non empty set containing one element is transitive.

21. State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive. [Delhi]
Answer:
As (1, 2) ∈ R, (2, 1) ∈ R, but (1, 1) ∉ R.

22. Consider the set A containing n elements, then the total number of injective functions from set A onto itself is _____ .
Answer:
Total number of injective functions from set containing n elements to a set containing n elements is ⁿ P_n = n!

23. The domain of the function f : R → R defined by f(x) = 4−x2−−−−−√ is ______ .
Answer:
[-2, 2]. For domain 4 – x² ≥ 0
⇒ 4 ≥ x²
⇒ x² ≤ 4
⇒ x² ≤ (2)²
⇒ -2 ≤ x ≤ 2, i.e. [-2, 2].

24. Let A = {a, b }. Then number of one-one functions from A to A possible are
(a) 2
(b) 4
(c) 1
(d) 3
Answer:(a) as if n(A) = m, then possible one-one functions from A to A are m!

25. Let A = {1, 2, 3, 4} and B = {a, b, c}. Then number of one-one functions from A to B are ______.
Answer:
0, as n(A) > n(B)

[sc name=”article1″ ]

26. If n(A) = p, then number of bijective functions from set A to A are ______ ..
Answer:
p!, as for bijective functions from A to B, n(A) = n(B) and function is one-one onto.

27. The function f : R → R defined as f(x) = [x], where [x] is greatest integer ≤ x, is onto function. State true or false.
Answer:
False, as range of f is set of integers, i.e.
Z and range of f ⊆ co-domain R. Hence,not onto e.g. for 12 ∈ R (co-domain) there is no x ∈ R (domain) such that y = f(x) or 12 e∈ R has no pre-image.

28. If \(f(x)=\frac{x-1}{|x-1|}, x(\neq 1) \in R\) then range of ‘f’ is _______ .
Answer:

29. If f : R → R be defined by f(x) = (3 – x³)^1/3, then find fof(x). [NCERT] 12 Maths MCQs
Answer:

Class 12 Maths MCQs with Answers Chapter 1 Relations and Functions – 12 Maths MCQs

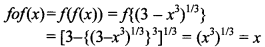
30. If f is an invertible function defined as f(x) = 3x−45, write f^-1(x).
Answer:

31. Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. State whether f is one-one or not. [AI 2011] f
Answer:
Explanation: One-one, as for x₁ ≠ x₂
⇒ f(x₁) ≠ f(x₂).

32. Let f : R → R is defined by f (x) = | x |. Is function f onto? Give a reason. [HOTS]
Answer:
f is not onto, as for some y ∈ R from co-domain, there is no x ∈ R from domain such that y = f(x), e.g. for -2 ∈ R (co-domain) there is no x ∈ R (domain) such that f(x) = -2, i.e. |x| = -2. Hence, not onto.

33. If f : R → R and g : R → R are given by f (x) = sin x and g(x) = 5x², find gof(x).
Answer:
gof(x) = g(f(x)) = g(sin x) = 5 sin² x.

34. Let f : {1, 3,4} → {1,2, 5} and g: {1,2, 5} → {1, 3} be given by f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}. Write down gof. [NCERT]
Answer:
gof: {1, 3, 4} → {1, 3}.
gof(1) = g(f(1)) = g(2) = 3.
gof(3) = g(K3)) = g(5) = 1
gof(4) = g(f(4)) = g(1) = 3
gof = {(1, 3), (3, 1), (4, 3)}.

12 Maths MCQs All Chapter with Answer

12 Maths MCQs for all Chapter NCERT text book and other books MCQs

35. Prove that f : R → R given by f(x) = x³ + 1 is one-one function.
Answer:
Given f(x) = x³ + 1
For x₁ ≠ x₂
⇒ x₁³ ≠ x₂³
⇒ x₁³ + 1 ≠ x₂³ + 1
⇒ f(x₁) ≠ f(x₂). Hence, one-one

36. Show that the Signum Function f : R → R,

one-one nor onto.

Answer:

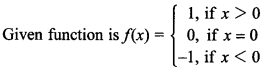
Range of function is {-1, 0, 1} and co-domain is set of real numbers R.
⇒ Range ⊆ co-domain.
There is at least one element in R(codomain) which is not image of any element of the domain, e.g. for 2 e R(co-domain), there is no x in domain such that f(x) = 2, x ∈ R.
Hence, function is not onto.
Also, let x₁ = 2 and x₂ = 3 then f(x₁) = 1 and f(x₂) = 1
i.e., x₁ ≠ x₂ ⇒ f(x₁) = f(x₂).
So, function is not one-one.

Given f(x) = sin x check if function f is one-one for (i) (0, π) (ii) (-π2, π2).
Answer: 12 Maths MCQs

38. If f : R → R is defined by f(x) = 3x + 2, define f (f(x)). [Foreign]
Answer:
f(f(x)) = f(3x + 2) = 3(3x + 2) + 2
= 9x+ 8.

39. Write fog, if f : R → R and g : R → R are given by f(x) = |x| and g(x) = |5x – 2|. [Foreign]
Answer:
(fog)(x) =f(g(x))
=f(|5x-2|) = ||5x-2||.

40. Write fog, if f : R → R and g : R → R are given by f(x) = 8x³ and g(x) = x^1/3. [Foreign]
Answer:
(fog)(x) = f(g(x)) = f(x^1/3) = 8(x^1/3)³ = 8x.

Class 12 Maths MCQs with Answers Chapter 1 Relations and Functions

12 Maths MCQs All Chapter with Answer

Facebook

Download PDF