Class 6 Maths Chapter 3 Important Questions

Class 6 Maths Chapter 3 Important Questions: Class 6 Maths Chapter 3 Playing With Numbers provided here can be used for the 2024-25 exam preparation.

Page Contents

Class 6 Maths Chapter 3 Important Questions

Multiple Choice Questions:

What are the numbers which have more than two factors called?

Even numbers
Prime numbers
Composite numbers
Odd numbers

The sum of two odd and one even numbers is:

Even
Prime
Composite
Odd

The number which is divisible by 5 is:

The HCF of 12 and 40 is:

Every ______ of a number is greater than or equal to that number.

factor
number
multiple
none to these

What is the H.C.F. of two co-prime numbers?

The LCM of 12, 15, 45 is:

Find the HCF of 27, 63.

______ is the smallest prime number which is even:

If a number is divisible by 10, then which of the following can be its one’s digit?

The value of 10 + 40 ÷ 8 × 2 – 9 is:

The number which is divisible by 3 is:

The only prime number which is also even is

Which of the following is the L.C.M. of 36 and 72?

A prime number is a number which:

is divisible by 2
is not divisible by 2
has no factors
has exactly two factors

Multiple Choice questions:

C. Composite numbers
A. Even
D. 425

Explanation: 425, a number is divisible by 5 if its unit’s digit is either 0 or 5.

B. 4

Explanation: 4,

2 × 2 × 3

HCF = 2 × 2 = 4

40 = 2 × 2 × 2 × 5

C. multiple
A. 1
B. 180

Explanation: 180

MCQ Questions for Class 6 Maths Chapter 3 Playing with Numbers with Answers 2

LCM = 2 × 2 × 3 × 3 × 5 = 180

D. 9
A. 2
D. 0
C. 11

Explanation: 10 + 40 ÷ 8 × 2 – 9 = 10 + 5 × 2 – 9 = 10 + 10 – 9 = 20 – 9 = 11 (BODMAS Rule)

A. 135

Explanation: 135, 1 + 3 + 5 = 9 which is divisible by 3 therefore no. is divisible

C. 2
B. 72
D. has exactly two factors

Explanation: Exactly two factors are 1 and the number itself.

Match The Following:

	Column I		Column II
1.	15	A.	Factor of 50
2.	12	B.	Factor of 30
3.	25	C.	Factor of 65
4.	13	D.	Factor of 48

Match The Following:

	Column I		Column II
1.	15	B.	Factor of 30
2.	12	D.	Factor of 48
3.	25	A.	Factor of 50
4.	13	C.	Factor of 65

Fill in the blanks:

1 is neither _____ nor _____.
The smallest prime number is _____.
The smallest composite number is _____.
The smallest even number is _____.

Fill in the blanks:

1 is neither prime number nor composite number.
The smallest prime number is 2.
The smallest composite number is 4.
The smallest even number is 2.

True /False:

A number with 4 or more digits is divisible by 8, if the number formed by the last three digits is divisible by 8.
If the sum of the digits of a number is divisible by 3, then the number itself is divisible by 9.
All numbers which are divisible by 4 may not be divisible by 8.
The Highest Common Factor of two or more numbers is greater than their Lowest Common Multiple.

True /False:

True
False
True
False

Very Short Questions:

Find LCM of 60 and 40.
Write all the factors of the following number: 27
List all the multiples of 7 that lie between 125 and 142.
Find the H.C.F of the following numbers. 70, 105, 175
Find the H.C.F of the following numbers. 27, 63
Find all the multiples of 9 upto 100.
Find the least 4-digit number which is exactly divisible by 8, 10, and 12.
What is the sum of any two?
(a) even numbers
(b) odd numbers
Which of the following numbers is divisible by 3?
(a) 1212
(b) 625
If the LCM and HCF of any two numbers are 15 and 4 respectively, find the product of the numbers.
Find the HCF of 5 and 7.
Write first 3 multiples of 25.
What are the possible factors of (a) 12 (b) 18?
Write first three multiples of 11.
Write pairs of twin prime numbers less than 20.

Very Short Answer:

Class 6 Maths Chapter 3 Important Questions – Class 6 Maths Chapter 3 Important Questions

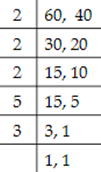
LCM = 2³ × 3 × 5 = 120

27 = 1 × 27

27 = 3 × 9

Thus, all the factors of 27 are 1, 3, 9 and 27.

By checking all the numbers from 125 to 142 which are divisible by 7, we get 126, 133, 140.

So, the multiples of 7 that lie between 125 to 142 are 126, 133 and 140.

Factors of 70 are 1, 2, 5, 7, 10, 14, 35 and 70.

Factors of 105 are 1, 3, 5, 7, 15, 21, 35 and 105.

Factors of 175 are 1, 5, 7, 25, 35 and 175.

∴ Common factors of 70, 105 and 175 are 1,5,7 and 35.

Highest of these common factors is 35.

∴ H.C.F of 70, 105 and 175 is 35.

Factors of 27 are 1, 3, 9 and 27.

Factors of 63 are 1, 3, 7, 9, 21 and 63.

∴ Common factors of 27 and 63 are 1, 3 and 9.

Highest of these common factors is 9.

∴ H.C.F. of 27 and 63 is 9.

The multiples of 9 are:

9 × 1 = 9, 9 × 2 = 18, 9 × 3 = 27, 9 × 4 = 36, 9 × 5 = 45, 9 × 6 = 54, 9 × 7 = 63, 9 × 8 = 72, 9 × 9 = 81, 9 × 10 = 90, 9 × 11 = 99, 9 × 12 = 108

Since 108 is greater than 100 therefore all the multiples of 9 upto 100 are 9, 18, 27, 36, 45, 54, 63, 72, 81, 90 and 99.

The smallest 4-digit number is 1000.

The least number which is exactly divisible by 8, 10, and 12 will be their L.C.M.

L.C.M. of 8, 10, and 12:

L.C.M. of 8, 10, 12 = 2 × 2 × 2 × 5 × 3 = 120.

By dividing smallest 4-digit number 1000 by 120,

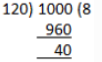
We find that 1000 is not exactly divisible by 120.

If we subtract 40 from 1000, we get 1000 – 40 = 960, which will be divisible by 120. But 960 is a 3-digit number. The next number to 960 which is divisible by 120 is 960 + 120 = 1080.

Therefore, the required 4-digit number divisible by 8, 10, and 12 is 1080.

(a) The sum of any two even numbers is even.

Example: 4 (even) + 6 (even) = 10 (even)

(b) The sum of any two odd numbers is even.

Example: 5 (odd) + 7 (odd) = 12 (even)

(a) Given number = 1212

Sum of the digits = 1 + 2 + 1 + 2 = 6, which is divisible by 3.

Hence, 1212 is also divisible by 3.

(b) Given number = 625

Sum of the digits = 6 + 2 + 5 = 13, which is not divisible by 3.

Hence, 625 is not divisible by 3.

We know that the product of the number = LCM × HCF = 15 × 4 = 60

Hence, the product of the given numbers = 60

Given numbers are 5 and 7. We observe that 5 and 7 are co-prime numbers.

Hence, the HCF is 1.

We have 25 × 1 = 25; 25 × 2 = 50; 25 × 3 = 75

Hence, the required multiples are 25, 50 and 75.

(a) Possible factors of 12 are:

12 = 1 × 12; 12 = 2 × 6; 12 = 3 × 4

Hence, the factors of 12 are 1, 2, 3, 4, 6 and 12.

(b) Possible factors of 18 are:

18 = 1 × 18; 18 = 2 × 9; 18 = 3 × 6

Hence, the factors of 18 are 1, 2, 3, 6, 9 and 18.

First three multiples of 11 are:

11 x 1 = 11; 11 x 2 = 22; 11 x 3 = 33

Hence, the required multiples are: 11,22 and 33.

Pairs of twin prime numbers are: (3, 5), (5, 7), (11, 13), (17, 19).

Short Questions:

Simplify: 32 + 96 ÷ (7 + 9)
Simplify: 18 + {1 + (5 – 3) x 5}
Without actual division, show that 11 is a factor of 1,10,011.
The sum of two numbers is 25 and their product is 144. Find the numbers.
Is 80136 divisible by 11?
The HCF and LCM of two numbers are 6 and 120 respectively. If one of the numbers is 24, find the other number.
Find the LCM of 12 and 30.
Find the smallest 4-digit number which is divisible by 18, 24 and 32.
Find the greatest number which divides 82 and 132 leaving 1 and 6, respectively as remainders.
Find the greatest number that will divide 455, 582 and 710 leaving remainders 14, 15 and 17 respectively.

Short Answer:

Given that: 32 + 96 ÷ (7 + 9)

= 32 + 96 ÷ 16 (Using BODMAS)

= 32 + 6 = 38

Given that: 18 + {1 + (5 – 3) × 5} (Using BODMAS)

= 18 + {1 + 2 × 5} = 18 + {1 + 10}

= 18 + 11 = 29.

Here 1,10,011 = 1,10,000 + 11

= 11 × 10,000 + 11 × 1

= 11 × (10,000 + 1)

= 11 × 10,001

It is clear that 11 is a factor of 11 × 10,001.

Hence, 11 is a factor of 1,10,011

The product of two numbers is 144.

∴ The possible factors are 1 × 144, 2 × 72, 3 × 48, 4 × 36, 6 × 24, 8 × 18, 9 × 16, 12 × 12

Here, we observe that out of these factors, we take 9 and 16.

Product = 9 × 16 = 144 and sum = 9 + 16 = 25

Hence, the required numbers are 9 and 16.

Sum of the digits at odd places = 6 + 1 + 8 = 15

Sum of the digits at even places = 3 + 0 = 3

Difference of the two sums = 15 – 3 = 12,

which is neither 0 nor the multiple of 11.

Hence, 80136 is not divisible by 11.

Given that: HCF = 6

LCM = 120

Let the two numbers be a and b, where a = 24, b = ?

We know that: a × b = HCF × LCM

⇒ 24 × b = 6 × 120

⇒ b = 6 × 12024

⇒ b = 30

Hence, the other number is 30.

Given numbers are 12 and 30

12 = 2 × 2 × 3;

30 = 2 × 3 × 5

∴ LCM = 2 × 2 × 3 × 5 = 60

Hence, the LCM of 12 and 30 = 60.

Given numbers are 18, 24 and 32, we have

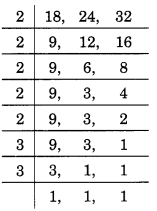
Thus, LCM = 2 × 2 × 2 × 2 × 2 × 3 × 3 = 288

The smallest 4-digit number = 1000

Now, we write multiples of 288, till we get a 4-digit number.

288 × 1 = 288, 288 × 2 = 576,

288 × 3 = 864, 288 × 4 = 1152

Hence, 1152 is the required number.

Given numbers are 82 and 132 and the remainders are 1 and 6 respectively.

We have, 82 – 1 = 81 and 132 – 6 = 126

So, we need to find the HCF of 81 and 126

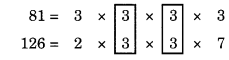
Common factor is 3 (occurring twice).

∴ HCF = 3 × 3 = 9

Hence, the required number is 9.

Given numbers are 455, 582 and 710 and the respective remainders are 14, 15 and 17.

We have 455 – 14 = 441, 582 – 15 = 567 and 710 – 17 = 693.

Now let us find their HCF.

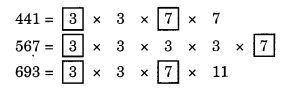
Common factors are 3 and 7.

∴ HCF = 3 × 7 = 21

Hence, the required number is 21.

Long Questions:

Three sets of English, Hindi, and Urdu books are to be stacked in such a way that the books are stored subject wise and the height of each stack is the same. The numbers of English, Hindi and Urdu books are 336, 192 and 144 respectively. Assuring that the books have that same thickness, determine the number of stacks of English, Hindi and Urdu books.
Ill cows, 185 sheep and 296 goats are to be taken across a river. There is only one boat and the boatsman says; he will take the same number and same kind of animals in each trip. Find the largest number of animals in each trip and the number of trips he will have to make.
In a seminar, the number of participants in Mathematics, Physics and Chemistry are 60, 96 and 144 respectively. Find the number of rooms required if in each room, the same number of ‘ participants are to be seated and all of them are to be in the same subject.

Long Answer:

Using BODMAS Rule, we have

40 + [20 – {28 ÷ 7 – 3 + (30 – 5 of 4)}]

= 40 + [20 – {28 ÷ 7 – 3 + (30 – 20)}]

= 40 + [20 – {28 ÷ 7 – 3 + 10}]

= 40 + [20 – [4 – 3 + 10}]

= 40 + [20-11] = 40 + 9 = 49.

To arrange the books in the required way,

we have to find the greatest number that divides 336, 192 and 144 exactly.

So, HCF of 336, 192 and 144 is

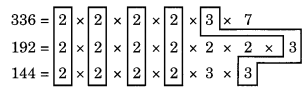
Common factors are 2 × 2 × 2 × 2 × 3 = 48

∴ HCF = 48, i.e., each stack contains 48 books.

∴ Number of stacks of English books = 336 + 48 = 7

Number of stacks of Hindi books = 192 4 – 48 = 4

Number of stacks of Urdu books = 144 4 – 48 = 3

We have

Number of cows = 111

Number of sheep = 185

Number of goats = 296

According to the condition of the boatsman, we need to find HCF of 111, 185 and 296

111 = 3 × 37;

185 = 5 × 37;

296 = 2 × 2 × 2 × 37

∴ the HCF = 37

So, the number of animals of same kind = 37.

Number of trips

=11137 +18537 +29637

= 3 + 5 + 8 = 16

Hence, the number of animals in each trip = 37

and the number of trips = 16

The number of participants in each room must be the HCF of 60, 96 and 144.

∴ 60 = 2 × 2 × 3 × 5

96 = 2 × 2 × 2 × 2 × 2 × 3

144 = 2 × 2 × 2 × 2 × 3 × 3

HCF = 2 × 2 × 3 = 12

Number of rooms required

= 6012 + 9612 + 14412

= 5 + 8 + 12 = 25

Hence, number of participants = 12

in each room and number of rooms required = 25.

Assertion and Reason Questions:

Assertion (A) – The factors of 34 are 1, 2, 17 and 34 itself
Reason (R) – every factor is less than or equal to the given number.

Both A and R are true and R is the correct explanation of A
Both A and R are true but R is not the correct explanation of A
A is true but R is false
A is false but R is true

Assertion (A) –The factors of 8 are 1, 2, 4, 8.
Reason (R) – every factor of a number is an exact divisor of that number.

Both A and R are true and R is the correct explanation of A
Both A and R are true but R is not the correct explanation of A
A is true but R is false
A is false but R is true

Assertion and Reason Answers:

1) a) Both A and R are true and R is the correct explanation of A2) a) Both A and R are true and R is the correct explanation of A