NCERT Solutions, Question Answer and Mind Map for Class 12 Chemistry Chapter 4, “Chemical Kinetics,” is a study material package designed to help students understand the principles of chemical kinetics, the study of the rates of chemical reactions.
NCERT Solutions provide detailed explanations and answers to the questions presented in the chapter. The solutions cover all the topics in the chapter, including the rate of reaction, factors affecting the rate of reaction, order of reaction, and rate laws. They also provide tips on how to answer different types of questions, including short answer, long answer, and multiple-choice questions.

The question-answer section of the chapter covers a wide range of topics, from the factors affecting the rate of a chemical reaction to the collision theory and the Arrhenius equation. It also includes questions on the different types of reactions, such as first-order and second-order reactions, and their rate laws.
The mind map provides a visual representation of the key topics covered in the chapter, allowing students to understand the connections between different concepts and ideas. The mind map covers the different factors that affect the rate of a chemical reaction, the collision theory, and the different types of reactions and their rate laws.
NCERT Solution / Notes Class 12 Chemistry Chapter 4 Chemical Kinetics with Mind Map PDF Download
Introduction: The stream of chemistry that governs the rate of reactions along with their mechanisms is termed as Chemical kinetics derived from a Greek word meaning chemical movement.
A combination of two or more reactants to produce a new product is called a reaction.
Elementary Reaction: The reaction that occurs in a single step to give the product is called an elementary reaction.
Complex reaction: The reactions that occur as a result of the sequence of elementary reactions to give the product is called complex reactions.
Rate of reaction
The rate at which the concentration of reactant or product participating in a chemical reaction alters is called rate of reaction.
Rate of reaction = change in concentration/ time = (mol/litre)/time
Reactant (R) –> Product.
Rate [R]
Rate = k[R]
k = rate constant or velocity constant.
Let one mole of the reactant A produce one mole of the product B.
Let at time t1
[A]1 and [B]1 = Concentrations of A and B
Let at time t2
[R]2 and [P]2 = Concentrations of A and B
Rate of disappearance of A = Decrease in concentration of R / Time taken = -∆[A]/∆t
Rate of appearance of B = Increase in concentration of P / Time taken = +∆[B]/∆t
When two or more reactants combine with each other the molecules of the respective reactants collide with each other to form the product. The collision between the molecules increases with the increase in concentration of the reactants and thereby increases the rate of reaction.
A + B –> C + D
Here molecules of reactant A and B collide to produce molecules of product C and D.
Therefore we can conclude that rate of reaction is directly proportional to the concentration of the participating reactants.
Rate ∝ [A]x [B]y
Or Rate = k[A]x [B]y
Hg(l) + Cl2 (g) –> HgCl2(s)
Rate of reaction= -∆[Hg]/∆t = ∆[Cl2]/∆t = ∆[Hg Cl2]/∆t
Rate of Chemical Reaction
The rate of reaction is the change in concentration of a reactant or product in unit time.
- Alternatively, the rate of reaction can also be expressed as
“The rate of decrease in the concentration of any one of the reactants.”
“The rate of increase in the concentration of any one of the products.”
- Consider a hypothetical reaction, assuming that the volume of the system remains constant.
R → P
One mole of the reactant R produces one mole of the product P.
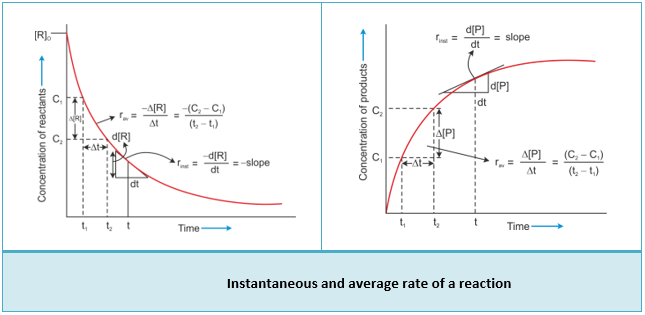
- If [R]1 and [P]1 are the concentrations of R and P at time t1 and [R]2 and [P]2 are their concentrations at time t2, then
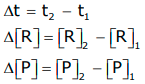
The square brackets in the above expressions are used to express molar concentration.

- Δ[R] is a negative quantity because the concentration of reactants is decreasing.

- Equations 1 and 2 represent the average rate of a reaction, rav.
This average rate depends on the change in concentration of reactants or products and the time taken for that change to occur.
Units of Rate of a Reaction
- From Equations 1 and 2, it is clear that the units of rate are concentration time−1.
- For example, if concentration is in mol L−1 and time is in seconds, then the units are mol L−1s−1.
- In gaseous reactions, the concentration of gases is expressed in terms of their partial pressures; hence, the units of the rate equation will be atm s−1.
Instantaneous Rate of Reaction
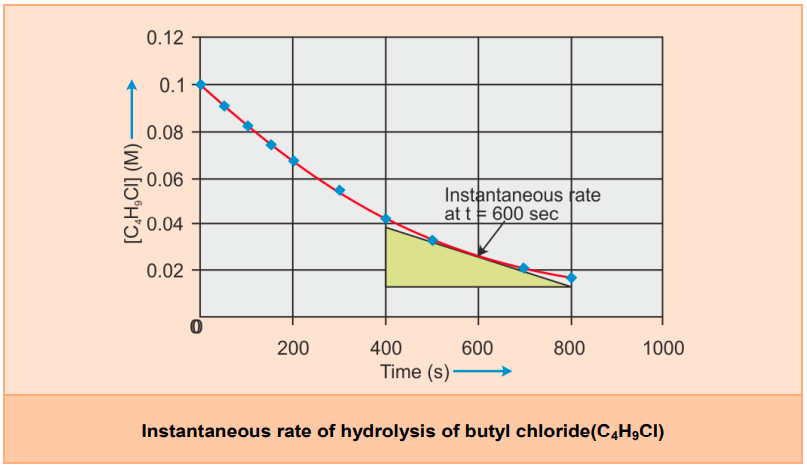
- Consider the hydrolysis of butyl chloride (C4H9Cl).
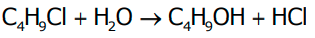
- We have provided the concentrations over different intervals of time below.

- We can determine the difference in concentration over different intervals of time, and thus, we determine the average rate by dividing Δ[R] by Δt.
- It can be seen from experimental data that the average rate falls from 1.90 × 10−4 mol L−1s−1 to 0.4 × 10−4 mol L−1s−1.
- However, the average rate cannot be used to predict the rate of reaction at a particular instant as it would be constant for the time interval for which it is calculated.
- Hence, to express the rate at a particular moment of time, we determine the instantaneous rate.
- It is obtained when we consider the average rate at the smallest time interval, say dt, when Δt approaches zero.
Therefore, for an infinitesimally small dt, the instantaneous rate is given by
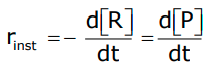
- By drawing the tangent at time t on either of the curves for the concentration of R versus time t or concentration of P versus time t and calculating the slope of the curve, we can determine the instantaneous rate of reaction.
- Hence, in this example, rinst at 600 s is calculated by plotting the graph of the concentration of butyl chloride as against time t.
- A tangent is drawn on the curve at a point t = 600 s.
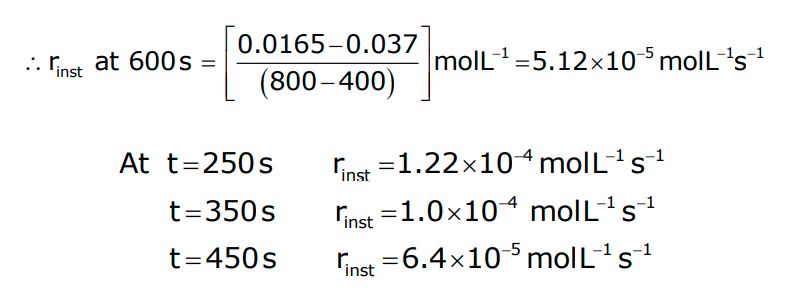
- Now consider a reaction,
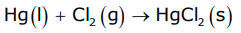
Here, the stoichiometric coefficients of the reactants and products are the same; hence, the rate of reaction is given as
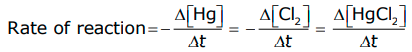
Therefore, we can say that from the above equation that the rate of disappearance of any of the reactants is the same as the rate of appearance of the products.
- Consider another reaction,
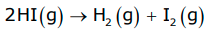
In this reaction, two moles of HI decompose to produce one mole each of H2 and I2, i.e. the stoichiometric coefficients of reactants or products are not equal to one; hence, we need to divide the rate of disappearance of any of the reactants or the rate of appearance of products by their respective stoichiometric coefficients.
Because the rate of consumption of HI is twice the rate of formation of H2 or I2, to make them equal, the term Δ[HI] is divided by 2.
The rate of this reaction is given by
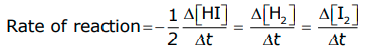
- For a gaseous reaction at constant temperature, concentration is directly proportional to the partial pressure of a species, and hence, the rate can be expressed as the rate of change in partial pressure of the reactant or the product.
Instantaneous rate of reaction
The ratio of change in concentration in chemical reaction to the time period is termed as instantaneous rate of the reaction.
-d[R]/dt = change in chemical concentration over short period of time/ the short time elapsed = (mol/litre) / time
It can be calculated from the slope of the tangent on a concentration- time graph.
For example, consider the following graph.
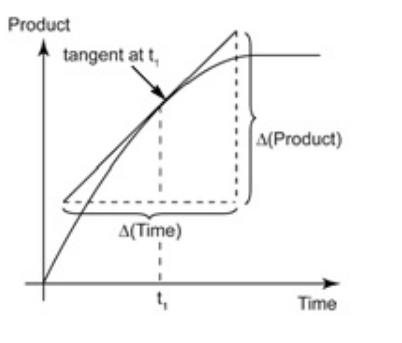
The rate of reaction at t = 40s in the above graph can be calculated by following method:
Rate of reaction = gradient of the tangent at 40s = (120-70)/(65-5) = 50/60= 0.83 cm3s-1
Rate of reaction
The rate at which the concentration of reactant or product participating in a chemical reaction alters is called rate of reaction.
Rate of reaction = change in concentration/ time = (mol/litre)/time
Reactant (R) –> Product.
Rate [R]
Rate = k[R]
k = rate constant or velocity constant.
Let one mole of the reactant A produce one mole of the product B.
Let at time t1
[A]1 and [B]1 = Concentrations of A and B
Let at time t2
[R]2 and [P]2 = Concentrations of A and B
Rate of disappearance of A = Decrease in concentration of R / Time taken = -∆[A]/∆t
Rate of appearance of B = Increase in concentration of P / Time taken = +∆[B]/∆t
When two or more reactants combine with each other the molecules of the respective reactants collide with each other to form the product. The collision between the molecules increases with the increase in concentration of the reactants and thereby increases the rate of reaction.
A + B –> C + D
Here molecules of reactant A and B collide to produce molecules of product C and D.
Therefore we can conclude that rate of reaction is directly proportional to the concentration of the participating reactants.
Rate ∝ [A]x [B]y
Or Rate = k[A]x [B]y
Hg(l) + Cl2 (g) –> HgCl2(s)
Rate of reaction= -∆[Hg]/∆t = ∆[Cl2]/∆t = ∆[Hg Cl2]/∆t
Average rate of reaction
The average rate of the reaction is the ratio of change in concentration of reactants to the change in time. It is determined by the change in concentration of reactants or products and the time taken for the change as well. As the reaction precedes forward the collisions between the molecules of the participating reactants reduces thereby decreasing the average rate of the reaction.
Mathematically, Average rate of reaction = Change in concentration / Time = (mol/litre)/time
Problem 1. For the reaction R → P, the concentration of a reactant changes from 0.03 M to 0.02 M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds.
Solution: R2= 0.02 M
R1= 0.03M
t2 – t1= 25 minutes
∆[R]/∆t =∆[R2-R1]/ t2- t1=- (0.02-0.03)/25 = 6.67 X 10-6 Ms-1
= 0.005ML-1 min-1
Problem 2. In a reaction, 2A → Products, the concentration of A decreases from 0.5 mol L-1 to 0.4 mol L-1 in 10 minutes. Calculate the rate during this interval?
Solution: -1/2 (∆[A]/∆t) =-1/2(∆[A2-A1]/∆t) =-1/2 (0.4-0.5/10)
=0.005ML-1 min-1
= 5 X 10-3M min-1
Rate expression
The representation of rate of reaction in terms of concentration of the reactants is called rate equation or rate expression.
For example, in the reaction
2NO(g) + O2(g) –> 2NO2
The rate expression is given as
Rate =k[NO]2[O2]
Let us consider another reaction
BrO3– + 5Br– + 6H+ –> 3Br + 3 H2O
Rate expression for this reaction is given as
k[BrO3–][Br–][H+]2
Order of a Reaction
The order of a reaction is defined as:
the sum of the powers to which the concentration terms are raised in the rate law equation to express the observed rate of the reaction.
The power of the concentration of a particular reactant in the rate law is called the order of the reaction with respect to that reactant.
If the rate of a reaction,
aA + bB + cC ——> Products
is given by the rate law as:
k[A]p [B]q [C]r
Rate = -dx /dt = k[A]p [B]q [C]r
then, the order of the reaction, n, is n = p+q+r
where p, q and r are the orders with respect to individual reactants and overall order of the reaction is sum of these exponents, i.e., p + q +r.
When n =1, the reaction is said to be first order reaction, if n = 2, the reaction is said to be second order reaction and so on.
Some Examples of Reactions of Different Orders
(a) Reactions of first order
(1) Decomposition of nitrogen pentoxide (N2O5)
2N2O5 (g) ——–> 2 NO2 (g) + ½ O2 (g)
Rate = k [N2O5]
(2) Decomposition of ammonium nitrite in aqueous solution
NH4NO2 ———>N2+2H2O
Rate = k[NH4NO2]
(3) Decomposition of H2O2 in the presence of I¯ ions
H2O2 ———-> H2O + ½ O2
Rate = k [H2O2]
(b) Reactions of second order
(1) Decomposition of nitrogen peroxide
2NO2 ——-> 2NO + O2
Rate =k [NO2]2
(2) Reaction between H2 and I2 to give HI
H2 + I2 ——–> 2HI
Rate =k[H2] [I2]
(c) Reactions of third order
(1) Reaction between nitric oxide and oxygen
2NO + O2 ——-> 2NO2
Rate = k [NO]2 [O2]
(2) Reaction between nitric oxide and Cl2
2NO +Cl2 ——>2NOCl
Rate = k [NO]2 [Cl2]
(d) Reactions of fractional order
(1) Decomposition of acetaldehyde is a fractional order reaction
CH3CHO ——-> CH4 + CO
Rate = k [CH3CHO]3/2
Order = 3/2 or 1.5
(2) The reaction between hydrogen and bromine to form hydrogen bromide is a fractional order reaction.
H2(g) + Br2(g)——> 2HBr
Rate = k [H2] [Br2]½
Order = 1 + ½ = 1½
(e) Zero order reaction
A number of zero order reactions are known in which the rate of the reaction is independent of the concentration of the reactants.
For example: the decomposition of ammonia at the surface of metals like gold, platinum etc., is a zero order reaction.
2NH3 ——–> N2 + 3H2
The rate of the reaction is independent of the concentration of ammonia, i.e.,
Rate = -dx/dt = k[NH3 ]0
Rate = k
order =0
Molecularity of a Reaction
For a chemical reaction to occur, the reacting molecules must collide with each other. The number of reacting species (molecules, atoms or ions) which collide simultaneously to bring about a chemical reaction is called molecularity of a reaction.
If a reaction involves the decomposition of only a single species, the molecularity is one or it is called unimolecular reaction.
For example:
1) The decomposition of hydrogen peroxide involves single species which undergoes the change to form the products. Hence, it is a unimolecular reaction.
H2O2 ——–> H2O + ½ O2
2) Decomposition of ammonium nitrite
NH4NO2 ——-> N2 + 2H2O
If the reaction involves the collision of two species, it is bimolecular and if three species take part in a collision leading to the formation of the products it is called trimolecular and so on.
The examples of bimolecular reactions are given below:
1) Dissociation of hydrogen iodide is a bimolecular reaction because two molecules collide to bring about the reaction.
2HI (g) ——-> H2 (g) + I2 (g)
2) Combination of NO and O3 is a bimolecular reaction
NO(g) + O3 (g) ——-> NO2 (g) + O2 (g)
The examples of trimolecular reactions are
The reaction of nitric oxide and oxygen is a trimolecular reaction because it involves collision of three reacting molecules.
2NO(g) + O2 (g) ——-> 2 NO2 (g)
Reactions involving three or more molecules are uncommon because such reactions requires the simultaneous collision of three or more than three molecules.
Simultaneous collision of three molecules means that the third molecule must collide the other two molecules at the same time when they are in the process of collision. The chances of the occurrence of such collisions are very small.
Some reactions involving more than three molecules are quite fast.
For example:
a) The reaction of bromide ions with bromate ions in the presence of an acid:
5Br¯ (aq) +BrO3‾ (aq) +6H+ (aq) ——-> 3 Br2 (aq) + 3H2O (l)
The experimentally measured rate law for this reaction is given as:
Rate = k[Br¯] [BrO3¯] [H+]2
This rate is first order with respect to Br¯ and BrO3¯ ion and second order with respect to H+ ions and the overall order of the reaction is 1+1+2=4.
b) The reaction of potassium chlorate with ferrous sulphate in the presence of sulphuric acid involves ten species.
KClO3+ 6FeSO4 + 3H2SO4 ——>KCl + 3Fe2(SO4)3 +3H2O
The above reaction appears to be of tenth order but actually it is a second order reaction. If this reaction were to take place in a single step, the 10 particles (1 KClO3 , 6 FeSO4 , and 3 H2SO4) would have to collide simultaneously.
But chances of such events are extremely small, so much so that a reaction which takes place by such collision will not occur at all.
Type of reactions which take place through a sequence of two or more consecutive steps are called complex reactions.
The detailed description of various steps by which reactants change into the products is called mechanism of the reaction.
The steps which contribute to the overall reaction are called elementary processes.
Integrated Rate Expression
The concentration dependence of rate is called differential rate equation. Integrated rate equation gives a relation between directly measured experimental quantities i.e. concentrations at different times. The integrated rate equations are different for reactions of different orders.
The instantaneous rate of a reaction is given by differential rate law equations.
For example: For a general reaction
aA +bB —–> Products
the differential rate law equation is :
dx/dt = k[A]a [B]b
The differential form of rate law is transformed to integrated form of rate law by simple mathematics (calculus).
Zero Order Reaction
A reaction is said to be of zero order, if its rate is independent of the concentration of the reactants. Consider the general zero order reaction:
R ——–> Product
Let [R] be the concentration of the reactant R and k0 is the rate constant for the zero order reaction. For the zero order reaction, the rate of the reaction is independent of the concentration of R. Thus,
Rate= -dRdt=k0 R=k0
This form of rate law is known as differential rate equation, Rearranging the above equation,
-d [R] =k0 dt
Integrating the above equation
-∫ d[R] = k0 ∫ dt
-[R]= k0t + I
where I is the constant of integration. The value of I can be calculated from the initial concentration.
For example: the initial concentration of R be [R]0, at t=0
-[R]0 = k0 × 0 + I
I = – [R]0
– [R] = K0t – [R]0
K0t = [R]0 – [R]
[R] = -K0t + [R]0
If we plot a graph between [R] against t, we get a straight line with slope as -k0 and intercept equal to [R]0.
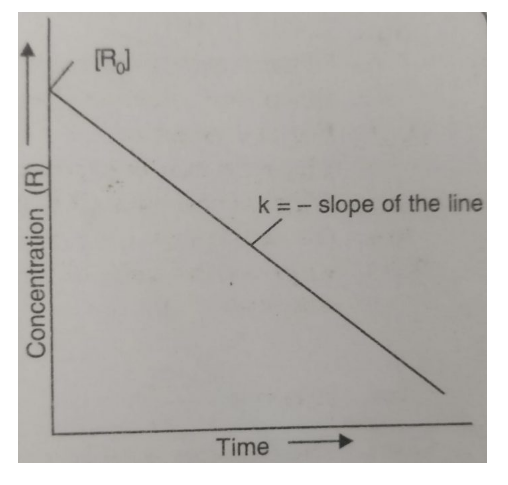
Alternatively, rate constant, k0 can be calculated if we know the concentration of R at any time t and [R]0. Thus,
k0 = { [R]0 – [R] } / t
where [R]0, is the initial concentration of R, [R] is the concentration at time t.
Alternatively, if the initial concentration of R is ‘a’ moles per litre and let x moles of reactants get changed to products in time t. Then, concentration of R left after time t be (a – x)
R ——-> Products
[R]0 =a
[R] = a – x so that
[R]0 -[R] = a- (a-x) = x
k0 = x/t
x=k0 t
The amount of the substance reacted is proportional to the time.
Zero order reactions generally take place in heterogeneous systems. In such systems the reactant is adsorbed on the surface of a solid catalyst, where it is converted into product. The fraction of the surface of the catalyst covered by the reactant is proportional to the concentration of the reactants at low values.
After certain concentration limit of the reactant, the surface of the catalyst becomes fully covered. On further increasing the concentration of the reactant, the reaction rate does not change. The rate becomes independent of the concentration and, therefore, becomes zero order reaction.
Collision Theory
Pseudo Chemical Reactions
Some reactions are first order each with respect to two different reactants i.e.,
A+B——-> Products
Rate = k[A] [B]
If one of the reactants is present in high concentration (solvent) then there is very little change in its concentration. The concentration of that reactant remains practically constant during the reaction.
For example, if [A] = 0.01 M and that of solvent water [B] = 55.5 M, the concentration of B changes only from 55.50 to 55.49 M even after the completion of the reaction.
The reaction, therefore, behaves as a first order reaction in A. Such reactions are called pseudo first order reactions.
Consider the hydrolysis of ethyl acetate:
CH3COOC2H5 + H2O ⇔ CH3COOH + C2H5OH
The molecularity of the reaction is two because it involves two reacting species, namely ethyl acetate and water. However, the concentration of ethyl acetate changes during the reaction while water is present in such a large excess that its concentration remains practically unchanged. Therefore, the rate of the reaction depends only the order of the reaction is one.
Rate = k’ [CH3COOC2H5] [H2O]
on the concentration of ethyl acetate and hence
[H2O] can be takes as constant so that
Rate = k [CH3COOC2H5]
k= k’ [H2O]
Thus, the reaction appears to be second order but follows the first order kinetics. Such reactions which appear to be of higher order but actually follow lower order kinetics are called pseudo chemical reactions.
For example: The hydrolysis of cane sugar or inversion of cane sugar to give glucose
and fructose:
C12H22O11 + H2O ——–> C6H12O6 + C6H12O6
Molecularity is two while order is one.
Collision Theory
Collision theory was put forward by Max Trautz and William Lewis in 1916-18. It is based on kinetic theory of gases.
According to this theory,
1) the reactant molecules are assumed to be hard spheres and reaction is postulated to occur when molecules collide with each other.
2) The number of collisions that takes place per second per unit volume of the reaction mixture is known as collision frequency Z. The value of collision frequency is normally very high.
3) For instance, under ordinary conditions of temperature and pressure, in a gaseous system, the collision frequency of binary collisions is of the order of 1025 to 1028.
4) If all the collisions are effective in forming the products, the reactions must be completed in a very short time.
5) All the collisions among the reacting species at a temperature are not effective in bringing about the chemical reaction.
The collisions which actually produce the products and therefore, result in the chemical reactions are called effective collisions.
There are two important barriers to a reaction namely
(i) energy barrier (ii) orientation barrier
(i) Energy barrier: For the reacting species to make effective collisions, they should have sufficient energy to break the chemical bonds in the reacting molecules. The minimum amount of energy which the colliding molecules must possess is known as threshold energy. This means that only those collisions of reactants will give products which possess energies greater than threshold energy.
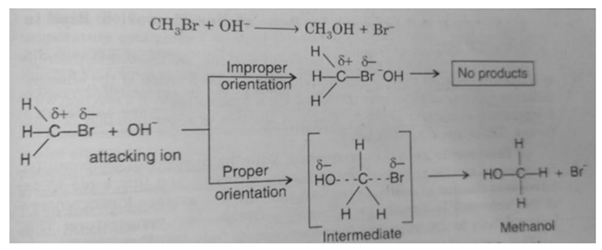
(ii) Orientation barrier: The colliding molecules should also have proper orientation so that the old bonds may break and new bonds are formed.
Consider the reaction
NO2 (g) + NO2 (g) ——> N2O4 (g)
During this reaction, the products molecules are formed only when the colliding molecules have proper orientation at the time of collisions. These are called effective collisions.
When the molecules do not have proper orientation at the time of collision, they result in ineffective collisions and do not form the products.
Effect of Catalyst on Reaction Rate
The rate of a reaction can be increased by raising the temperature. However, temperature can be raised within certain limits because in certain cases, the reactants become unstable at higher temperatures and decompose.
Many reactions are made to proceed at an increased rate by the presence of some other substance.
For example: a mixture of H2 and O2 does not react at room temperature. However, in the presence of finely divided platinum, the reaction becomes quite vigorous.
Manganese dioxide, a black powder speeds up the thermal decomposition of potassium chlorate.
2 KClO3 (s) ——–> 2KCl (s) + 3 O2
Catalysts
The substances which accelerate the rate of reactions without itself undergoing permanent change are called catalysts.
The substances which increase the rate of a reaction and can be recovered chemically unchanged in mass and composition after the reaction are called catalysts.
The phenomenon of increasing the rate of a reaction by the use of catalyst is called catalysis. A catalyst is not consumed in the reaction.
In a catalysed reaction the catalyst is used in one step and is regenerated in subsequent step and thus, it is used up again and again without undergoing any permanent change.
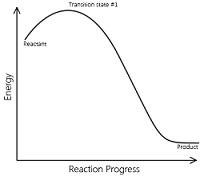
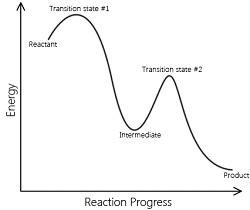
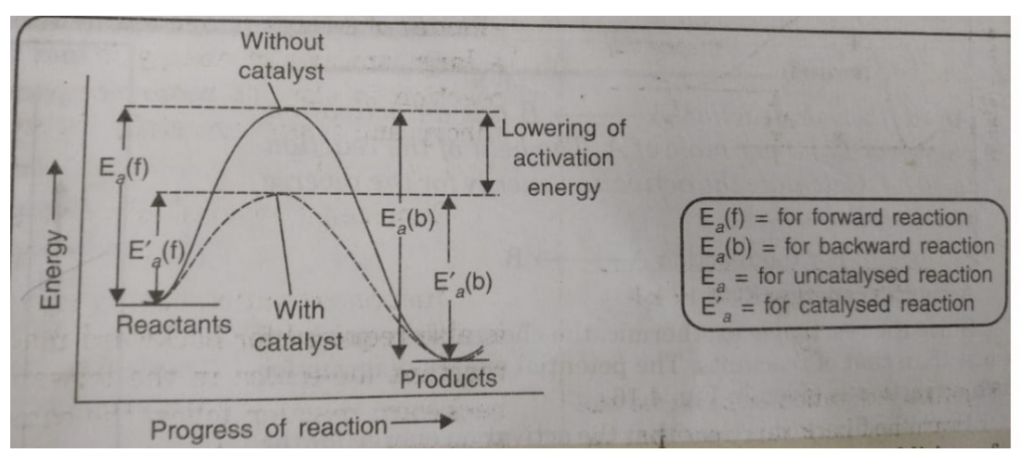
Catalyst provides an entirely new path for the reaction in which the reactants are converted to products quickly. The catalyst forms a new activated complex of lower potential energy. This means that the activation energy becomes lower for the catalysed reaction than that for uncatalysed reaction. The fraction of the total number of collisions possessing lower activation energy increased and hence, the rate of reaction also increase.
The solid line shows the path for uncatalysed reaction and dotted line shows the path adopted by catalysed reaction. Consider a hypothetical reaction
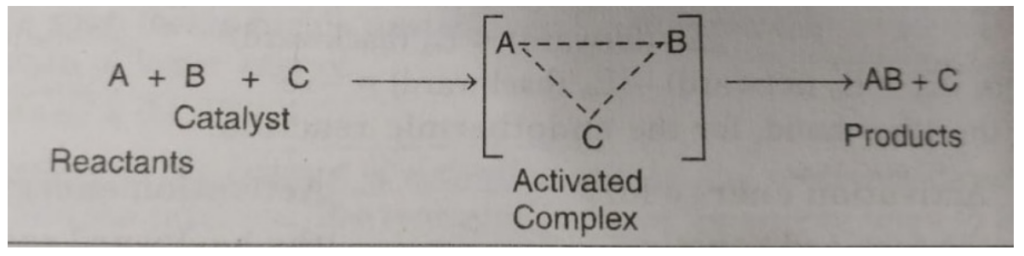
A + B ——–> AB
The reaction proceeds through the formation of activated complex
A+B ——> [A…B] ——> AB
Addition of a catalyst C result into the formation of new activated complex of lower activation energy.
The Function of Catalyst
(1) A catalyst may undergo intermediate physical changes and it may even form temporary chemical bonds with the reactants but it is recovered unchanged in original form at the end of the reaction.
(2) A catalyst speeds up the reaction but it does not shift the position of equilibrium. The presence of a catalyst reduces the height of barrier by providing an alternative path for the reaction and lowers the activation energy. The lowering in activation energy is to the same extent for the forward as well as for the backward reaction.
(3) Catalysts are highly specific in nature. A catalyst which can catalyse one reaction may have no effect on another reaction even, if that reaction is very similar.
(4) The catalyst does not change ΔE (or ΔH) of the reaction.
Half Life Period of a Reaction
Half life period of a reaction is defined as the time during which the concentration of a reactant is reduced to half of its initial concentration.
or
The time in which half of a reaction is completed. It is generally denoted as t½
The half life period of a first order reaction may be calculated as given below:
The first order rate equation for the reaction
A → Products
kt=2.303log A0[A]
t=2.303k=logA0[A]
Half life period of a reaction
Now, half life period corresponds to time during which the initial concentration, [A]0 is reduced to half i.e.
[A] = [A]0 /2 at t= t½
Then half life period, t½ becomes
t1/2 =2.303klog A0A0/2=2.303klog 2
t1/2 =2.303×0.3010k0.693k
t1/2 =0.693k
Half life period of a reaction
Thus, half life period of a first order reaction is independent of the initial concentration of the reactant. Half life period for the first order reaction is inversely proportional to the rate constant.
For example,
(i) time required to complete 1/3 of the reaction will be given as:
[A]o = a , [A] = a – a/3=2/3a
t1/3 =2.303klog a1/3a=2.303klog 32
time required to complete 1/3 of the reaction
(ii) time required to complete 3/4 of the reaction will be
[A]o = a , [A] = a – 3/4 a = 1/4 a
time required to complete 3/4 of the reaction
t3/4 =2.303klog a1/4a=2.303klog 4
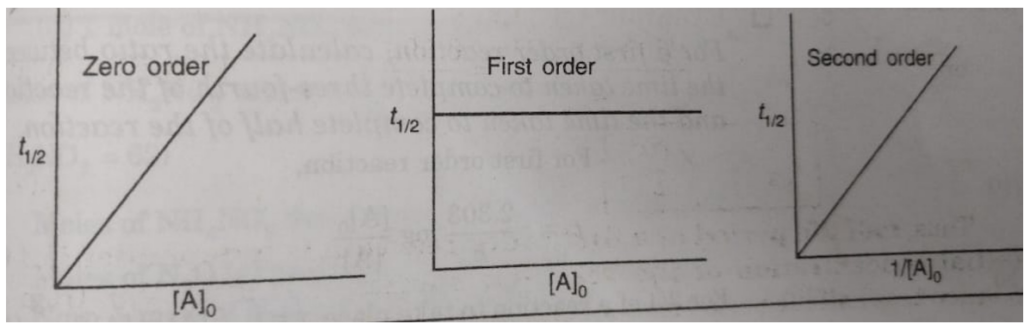
Half Life period of zero order and second order reactions
The integrated rate equation is ,
kt = [A]o -[A]
For half life period, t½ , [A] = [A]0/2
t½ = [A]0 /2k
Similarly for second order reaction,
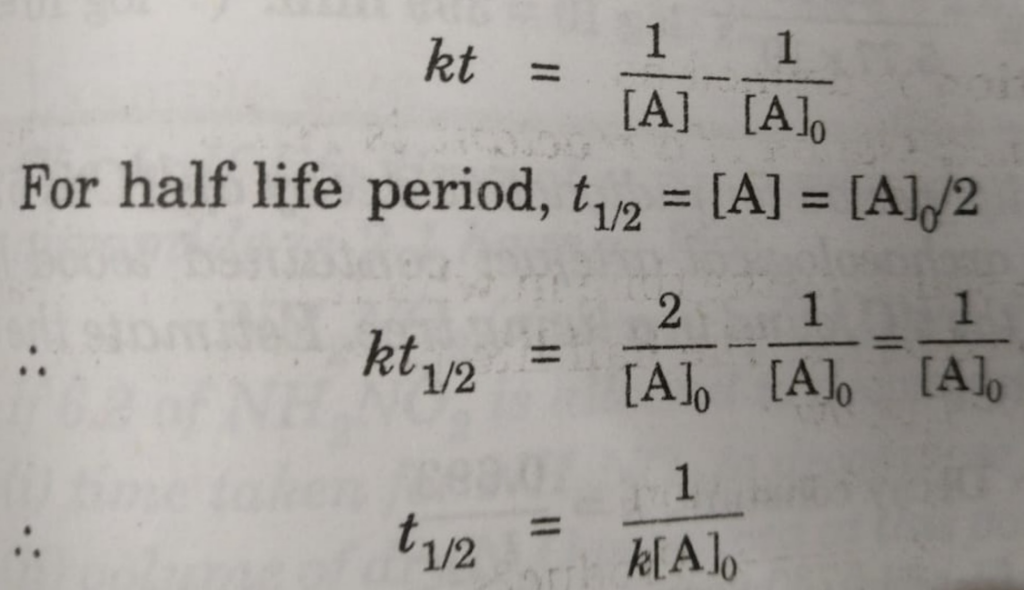
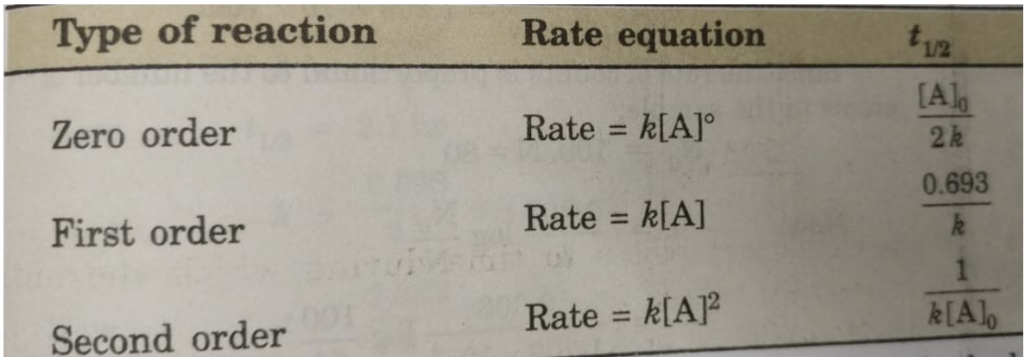
NCERT Solutions for Class 12 Chemistry chapter wise
- Chapter 1 The Solid State
- Chapter 2 Solutions
- Chapter 3 Electrochemistry
- Chapter 4 Chemical Kinetics
- Chapter 5 Surface Chemistry
- Chapter 6 General Principles and Processes of Isolation of Elements
- Chapter 7 The p Block Elements
- Chapter 8 The d and f Block Elements
- Chapter 9 Coordination Compounds
- Chapter 10 Haloalkanes and Haloarenes
- Chapter 11 Alcohols Phenols and Ethers
- Chapter 12 Aldehydes Ketones and Carboxylic Acids
- Chapter 13 Amines
- Chapter 14 Biomolecules
- Chapter 15 Polymers
- Chapter 16 Chemistry in Everyday Life
